题目内容
【题目】在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
【答案】3或![]()
【解析】
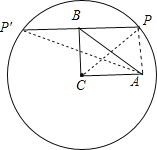
试题分析:连结CP,PB的延长线交⊙C于P′,如图,先计算出CB2+PB2=CP2,则根据勾股定理的逆定理得∠CBP=90°,再根据垂径定理得到PB=P′B=4,接着证明四边形ACBP为矩形,则PA=BC=3,然后在Rt△APP′中利用勾股定理计算出P′A=![]() ,从而得到满足条件的PA的长为3或
,从而得到满足条件的PA的长为3或![]() .
.
解:连结CP,PB的延长线交⊙C于P′,如图,
∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A=![]() =
=![]() ,
,
∴PA的长为3或![]() .
.
故答案为3或![]() .
.

练习册系列答案
相关题目