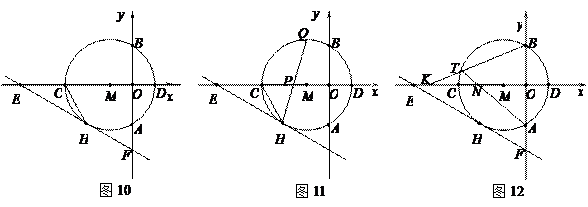Question

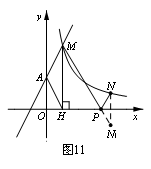
如图11，直线与y轴交于A点，与反比例函数（x＞0）的图象交

      于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2.

（1）求k的值；

（2）点N（a，1）是反比例函数（x＞0）图像上的点，

在x轴上是否存在点P，使得PM＋PN最小，若存

在，求出点P的坐标；若不存在，请说明理由.

Answer 1

（1）由y＝2x＋2可知A（0，2），即OA＝2.………………………………（1分）

∵tan∠AHO＝2，∴OH＝1.………………………………………………（2分）

∵MH⊥x轴，∴点M的横坐标为1.

∵点M在直线y＝2x＋2上，

∴点M的纵坐标为4.即M（1，4）.…………（3分）

∵点M在y＝上，∴k＝1×4＝4. …………（4分）

（2）∵点N（a，1）在反比例函数（x＞0）上，

     ∴a＝4.即点N的坐标为（4，1）.…………（5分）

过N作N关于x轴的对称点N₁，连接MN₁，交x轴于P（如图11）.

此时PM＋PN最小.         ………………………………………………（6分）

∵N与N₁关于x轴的对称，N点坐标为（4，1），

∴N₁的坐标为（4，－1）.……………………………………………………（7分）

设直线MN₁的解析式为y＝kx＋b.

由  解得k＝－，b＝.…………………………………（9分）

∴直线MN的解析式为.

令y＝0，得x＝. ∴P点坐标为（，0）.………………………（10分）