题目内容
如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,ED⊥AB于F,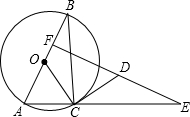
(1)求证:△CDE是等腰三角形;
(2)若AB=4,AE=2(
| 3 |
分析:(1)由于AB是直径,那么∠ACB=90°,而∠ABC=30°,易求∠BAC=60°,结合OA=OC,易证△AOC是正三角形,于是∠OCD=60°,结合CD是切线,易求∠DCE=30°,在Rt△AEF中,易求∠E=30°,于是∠DCE=∠E,可证△CDE实等腰三角形;
(2)在Rt△ABC中,由于∠A=60°,AB=4,易求AC=AO=2,利用勾股定理可求BC=2
,CE=AE-AC=2
,那么BC=CE,而∠OBC=∠OCB=∠DCE=∠DEC=30°,从而可证△OBC≌△DCE.
(2)在Rt△ABC中,由于∠A=60°,AB=4,易求AC=AO=2,利用勾股定理可求BC=2
| 3 |
| 3 |
解答:证明:(1)∵AB为直径,
∴∠ACB=90°,
又∠ABC=30°,
∴∠BAC=60°,
又∵OA=OC,
∴△AOC是正三角形,
又∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠DCE=180°-60°-90°=30°,
又∵ED⊥AB于F,
∴∠DEC=90°-∠BAC=30°,
∴∠DCE=∠DEC,
故△CDE为等腰三角形;
(2)在Rt△ABC中,
∵AB=4,AC=AO=2,
∴BC=
=2
,
而CE=2(
+1)-2=2
,
∴BC=CE,
又∵∠OBC=∠OCB=∠DCE=∠DEC=30°,
∴△OBC≌△DCE(ASA).
∴∠ACB=90°,
又∠ABC=30°,
∴∠BAC=60°,
又∵OA=OC,
∴△AOC是正三角形,
又∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠DCE=180°-60°-90°=30°,
又∵ED⊥AB于F,
∴∠DEC=90°-∠BAC=30°,
∴∠DCE=∠DEC,
故△CDE为等腰三角形;
(2)在Rt△ABC中,
∵AB=4,AC=AO=2,
∴BC=
| 42-22 |
| 3 |
而CE=2(
| 3 |
| 3 |
∴BC=CE,
又∵∠OBC=∠OCB=∠DCE=∠DEC=30°,
∴△OBC≌△DCE(ASA).
点评:本题考查了切线的性质、等边三角形的判定和性质、等腰三角形的判定、勾股定理、全等三角形的判定和性质.解题的关键是证明△AOC是正三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( )
7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( ) 如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F. 24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长.
24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长. (2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB. 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5