题目内容
 如图,∠P=36°,∠N=72°,MF为∠PMN的平分线,EF∥MN,则图中等腰三角形的个数是
如图,∠P=36°,∠N=72°,MF为∠PMN的平分线,EF∥MN,则图中等腰三角形的个数是
- A.5个
- B.4个
- C.3个
- D.2个
A
分析:根据等腰三角形的判定定理:在三角形中,如果两个底角相等,那么该三角形是等腰三角形.由此来判断图形中有几个等腰三角形.
解答:∵∠P=36°,∠N=72°
∴∠PMN=72°,△PMN为等腰三角形.
∵MF为∠PMN的平分线,∠P=36°
∴∠PMF=∠FMN=36°,△PMF为等腰三角形.
∵EF∥MN,
∴∠PFE=∠N=72°,∠PEF=∠PMN=72°
∴△PEF为等腰三角形.
∵EF∥MN,∠FMN=36°,∠N=72°
∴∠EFM=∠FMN=36°,∠MFN=72°
∴△MFN为等腰三角形.
∵∠PMF=∠FMN=36°,∠EFM=∠FMN=36°
∴∠EMF=∠EFM
∴△EMF为等腰三角形.
综上得出图形中的等腰三角形为:△PMN,△EMF,△MFN,△FPM,△PEF.
故选择A.
点评:本题考查了三角形的内角和为180°,平行线的性质定理,等腰三角形的判定定理;求得各角的度数是正确解答本题的关键.
分析:根据等腰三角形的判定定理:在三角形中,如果两个底角相等,那么该三角形是等腰三角形.由此来判断图形中有几个等腰三角形.
解答:∵∠P=36°,∠N=72°
∴∠PMN=72°,△PMN为等腰三角形.
∵MF为∠PMN的平分线,∠P=36°
∴∠PMF=∠FMN=36°,△PMF为等腰三角形.
∵EF∥MN,
∴∠PFE=∠N=72°,∠PEF=∠PMN=72°
∴△PEF为等腰三角形.
∵EF∥MN,∠FMN=36°,∠N=72°
∴∠EFM=∠FMN=36°,∠MFN=72°
∴△MFN为等腰三角形.
∵∠PMF=∠FMN=36°,∠EFM=∠FMN=36°
∴∠EMF=∠EFM
∴△EMF为等腰三角形.
综上得出图形中的等腰三角形为:△PMN,△EMF,△MFN,△FPM,△PEF.
故选择A.
点评:本题考查了三角形的内角和为180°,平行线的性质定理,等腰三角形的判定定理;求得各角的度数是正确解答本题的关键.

练习册系列答案
相关题目
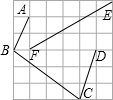 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.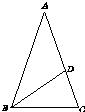 24、如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并说明理由.
24、如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并说明理由.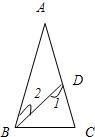 20、如图,∠A=36°,∠DBC=36°,∠C=72°,那么,∠1=
20、如图,∠A=36°,∠DBC=36°,∠C=72°,那么,∠1=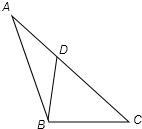
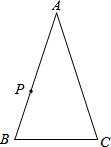 (2013•淄博)在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有
(2013•淄博)在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有