题目内容
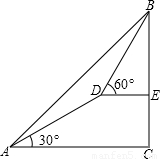
如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处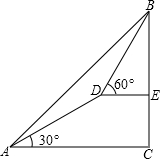 测得山顶B的仰角为60°,求山的高度?
测得山顶B的仰角为60°,求山的高度?
分析:根据题目所给的度数可判定△ABD是等腰三角形,AD=BD,然后解直角三角形,可求出BE的长和CE的长,从而可求出山高的高度.
解答: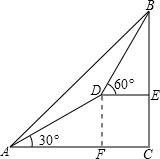 解:∵∠BAC=45°,∠DAC=30°,
解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DE⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=
AD=500,
∴EC=500,BE=1000×sin60°=500
.
∴BC=500+500
米.
 解:∵∠BAC=45°,∠DAC=30°,
解:∵∠BAC=45°,∠DAC=30°,∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DE⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=
| 1 |
| 2 |
∴EC=500,BE=1000×sin60°=500
| 3 |
∴BC=500+500
| 3 |
点评:本题考查直角三角形的应用仰角俯角问题,关键是根据角判断特殊的三角形,直角三角形或者等腰三角形,从而求出解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
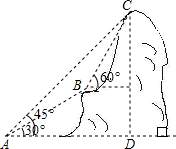 如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60度.已知C地比A地高200米,电缆BC至少长多少米?(精确到0.1米)
如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60度.已知C地比A地高200米,电缆BC至少长多少米?(精确到0.1米)