Question

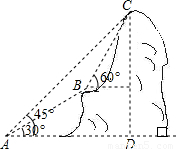
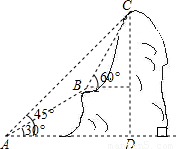
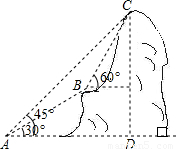
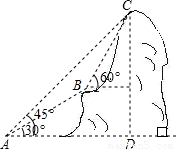
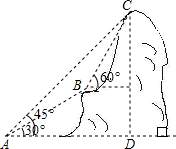如图，某电信部门计划修建一条连接B、C两地的电缆，测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B地测得C地的仰角为60度．已知C地比A地高200米，电缆BC至少长多少米？（精确到0.1米）

Answer 1

分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造方程关系式，进而可解即可求出答案．

解答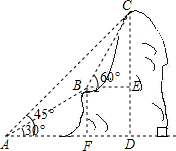：解：过B点分别作BE⊥CD、BF⊥AD，垂足分别为E、F．
设BC=xm．
∵∠CBE=60°，
∴BE=

1

2

x，CE=

3

2

x．
∵CD=200，
∴DE=200-

3

2

x．
∴BF=DE=200-

3

2

x，DF=BE=

1

2

x．
∵∠CAD=45°，
∴AD=CD=200．
∴AF=200-

1

2

x．
在Rt△ABF中，tan30°=

BF

AF

=

200- 3 2 x

200- 1 2 x

，
解得x=200（

3

-1）≈146.5（m）．
答：电缆BC至少146.5米．

点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．