题目内容
已知E是矩形ABCD的边BC的中点,那么S△AED=________S矩形ABCD( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:可先依据题意作出简单的图形,进而结合图形进行分析,题中ABCD是矩形,其面积为底边长与高的乘积,又点E是BC的中点,△ADE的高与矩形的高相等,底边长也相等,进而可得出结论.
解答: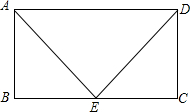 解:如图所示,
解:如图所示,
SABCD=AB•AD,S△ADE=
AB•AD,
故S△ADE=
SABCD,
故此题选A.
 解:如图所示,
解:如图所示,SABCD=AB•AD,S△ADE=
| 1 |
| 2 |
故S△ADE=
| 1 |
| 2 |
故此题选A.
点评:本题主要考查矩形的性质及三角形面积的计算,应熟练掌握.

练习册系列答案
相关题目
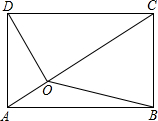 如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为( )
如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为( )| A、2 | ||
B、2
| ||
C、2
| ||
| D、3 |
 24、如图,已知P是矩形ABCD的内的一点.求证:PA2+PC2=PB2+PD2.
24、如图,已知P是矩形ABCD的内的一点.求证:PA2+PC2=PB2+PD2. 22、如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.
22、如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.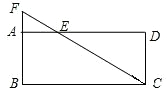 如图,已知E是矩形ABCD的边AD上的点,AE:ED=1:3,CE与BA的延长线交于点F.如果三角形AEF的面积为1,那么四边形ABCD的面积为
如图,已知E是矩形ABCD的边AD上的点,AE:ED=1:3,CE与BA的延长线交于点F.如果三角形AEF的面积为1,那么四边形ABCD的面积为