题目内容
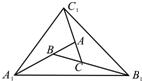18、如图，对面积为s的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；
第二次操作，分别延长A1B1、B1C1、C1A1至点A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，B2C1=2B1C1，顺次连接A2、B2、C2，得到△A2B2C2，记其面积为S2；
…；
按此规律继续下去，可得到△AnBnCn，则其面积Sn=
19nS
．分析：连接A1C，找出延长各边后得到的三角形是原三角形的19倍的规律，利用规律求延长第n次后的面积．
解答：解：连接A1C；
△AA1C=3△ABC=3，
△AA1C1=2△AA1C=6，
所以△A1B1C1=6×3+1=19；
同理得△A2B2C2=19×19=361；
△A3B3C3=361×19=6859，
△A4B4C4=6859×19=130321，
△A5B5C5=130321×19=2476099，
从中可以得出一个规律，延长各边后得到的三角形是原三角形的19倍，所以延长第n次后，得到△AnBnCn，则其面积Sn=19n•S．
△AA1C=3△ABC=3，
△AA1C1=2△AA1C=6，
所以△A1B1C1=6×3+1=19；
同理得△A2B2C2=19×19=361；
△A3B3C3=361×19=6859，
△A4B4C4=6859×19=130321，
△A5B5C5=130321×19=2476099，
从中可以得出一个规律，延长各边后得到的三角形是原三角形的19倍，所以延长第n次后，得到△AnBnCn，则其面积Sn=19n•S．
点评：本题的关键是作辅助线，连接A1C，找出延长各边后得到的三角形是原三角形的19倍的规律，利用规律求延长第n次后的面积．
练习册系列答案
相关题目
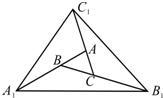17、如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB，BC，CA至点A1，B1，C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1，B1，C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2，B2，C2，得到△A2B2C2，记其面积为S2；…；按此规律继续下去，可得到△A5B5C5，则其面积S5=
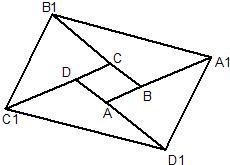8、如图，对面积为1的平行四边形ABCD逐次进行以下操作：第一次操作，分别延长AB，BC，CD，DA至点A1，B1，C1，D1，使得A1B=2AB，B1C=2BC，C1D=2CD，D1A=2AD，顺次连接A1，B1，C1，D1，得到平行四边形A1B1C1D1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1D1、D1A1至点A2，B2，C2，D2，使得A2B1=2A1B1，B2C1=2B1C1，C2D1=2C1D1，D2A1=2A1D1，顺次连接A2，B2，C2，D2记其面积为S2；…；按此规律继续下去，可得到平行四边形A5B5C5D5，则其面积S5=
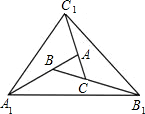如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1、B1C1、C1A1至点A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2、B2、C2，得到△A2B2C2，记其面积为S2；…；按此规律继续下去，可得到△A5B5C5，则其面积S5=
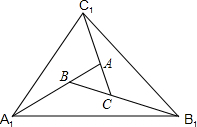（2012•门头沟区一模）如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1A1至A2，B2，C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2，B2，C2，得到△A2B2C2，记其面积为S2…，按此规律继续下去，可得到△A5B5C5，则其面积为S5=