题目内容
(2010•莆田质检)某课题组在探究“泵站问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题:
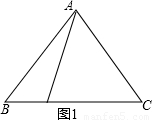
(1)几何应用:如图1,等腰直角三角形ABC的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为______
【答案】分析:(1)本题要在AC上找一点P,使PB+PE的值最小.设点B关于AC的对称点为B′,使PB+PE的值最小就是使PB′+PE的值最小.
(2)设点B关于AC的对称点为B′,根据垂线段最短及两点之间,线段最短可知当B′、M、N三点共线且B′N⊥AB时BM+MN的值最小.
(3)根据两点间距离公式,可知本题即求点P(x,0)(0≤x≤4)到点A(0,1)和点B(4,2)的距离之和的最小值,在平面直角坐标系中画出图形,即可求解.
解答:解:(1)作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小,连接AB′.

∵∠B′AC=∠BAC=45°,∴∠B′AB=90°.
又∵AB′=AB=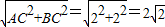 ,AE=
,AE=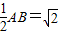 ,
,
∴PB+PE的最小值=B′E= .
.
(2)作点B关于AC的对称点B′,过B′作B′N⊥AB于N,交AC于M.
此时BM+MN的值最小.BM+MN=B′N.
理由:如图1,在AC上任取一点M1(不与点M重合),
在AB上任取一点N1,连接B′M1、BM1、M1N1、B′N1.

∵点B′与点B关于AC对称,
∴BM1=B′M1,
∴BM1+M1N1=B′M1+M1N1>B′N1.
又∵B′N1>B′N,BM+MN=B′N,
∴BM1+M1N1>BM+MN.
计算:如图2
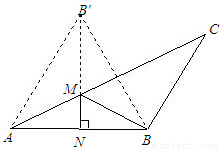
∵点B′与点B关于AC对称,
∴AB′=AB,
又∵∠BAC=30°,
∴∠B′AB=60°,
∴△B′AB是等边三角形.
∴B′B=AB=2,∠B′BN=60°.
又∵B′N⊥AB,
∴B′N=B′B•sin60°= .
.
(3)构造图形如图所示:

在直角坐标系中,设点A(0,1)、B(4,2)、P(x,0)(0≤x≤4).
那么PA+PB=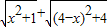 .
.
所求 的最小值就是求PA+PB的最小值.
的最小值就是求PA+PB的最小值.
作点A关于x轴的对称点A′,过A′作y轴的垂线,过点Bx轴的垂线,两垂线交于点C.
则A′C=4,BC=3,A′B=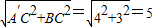 .
.
所求 的最小值是5.
的最小值是5.
点评:此题主要考查轴对称--最短路线问题.解这类问题的关键是将实际问题抽象或转化为数学模型,把两条线段的和转化为一条线段.
(2)设点B关于AC的对称点为B′,根据垂线段最短及两点之间,线段最短可知当B′、M、N三点共线且B′N⊥AB时BM+MN的值最小.
(3)根据两点间距离公式,可知本题即求点P(x,0)(0≤x≤4)到点A(0,1)和点B(4,2)的距离之和的最小值,在平面直角坐标系中画出图形,即可求解.
解答:解:(1)作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小,连接AB′.

∵∠B′AC=∠BAC=45°,∴∠B′AB=90°.
又∵AB′=AB=
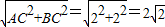 ,AE=
,AE=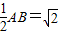 ,
,∴PB+PE的最小值=B′E=
 .
.(2)作点B关于AC的对称点B′,过B′作B′N⊥AB于N,交AC于M.
此时BM+MN的值最小.BM+MN=B′N.
理由:如图1,在AC上任取一点M1(不与点M重合),
在AB上任取一点N1,连接B′M1、BM1、M1N1、B′N1.

∵点B′与点B关于AC对称,
∴BM1=B′M1,
∴BM1+M1N1=B′M1+M1N1>B′N1.
又∵B′N1>B′N,BM+MN=B′N,
∴BM1+M1N1>BM+MN.
计算:如图2

∵点B′与点B关于AC对称,
∴AB′=AB,
又∵∠BAC=30°,
∴∠B′AB=60°,
∴△B′AB是等边三角形.
∴B′B=AB=2,∠B′BN=60°.
又∵B′N⊥AB,
∴B′N=B′B•sin60°=
 .
.(3)构造图形如图所示:

在直角坐标系中,设点A(0,1)、B(4,2)、P(x,0)(0≤x≤4).
那么PA+PB=
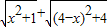 .
.所求
 的最小值就是求PA+PB的最小值.
的最小值就是求PA+PB的最小值.作点A关于x轴的对称点A′,过A′作y轴的垂线,过点Bx轴的垂线,两垂线交于点C.
则A′C=4,BC=3,A′B=
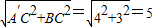 .
.所求
 的最小值是5.
的最小值是5.点评:此题主要考查轴对称--最短路线问题.解这类问题的关键是将实际问题抽象或转化为数学模型,把两条线段的和转化为一条线段.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 过A、C两点,直线AC与x轴相交于点E、与y轴相交于点F.
过A、C两点,直线AC与x轴相交于点E、与y轴相交于点F.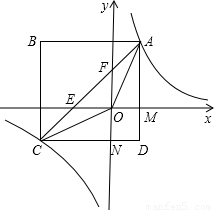
 ,而其每千克成本y2(元)与销售月份x(月)满足的函数关系y2=ax2-10ax+c,其图象如图所示.
,而其每千克成本y2(元)与销售月份x(月)满足的函数关系y2=ax2-10ax+c,其图象如图所示.
 ,若△ABD的面积为S1,△ABC的面积为S2,则S1:S2=______;
,若△ABD的面积为S1,△ABC的面积为S2,则S1:S2=______;