题目内容
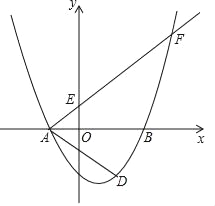
【题目】在平面直角坐标系xOy中,抛物线G:y=ax2-4ax+3a-2(a≠0),其顶点为C,直线l:y=ax-2a+1(a≠0)与x轴、y轴分别交于A,B两点.
(1)当抛物线G的顶点C在x轴上时,求a的值;
(2)当a>0时,若△ABC的面积为2,求a的值;
(3)若点Q(m,n)在抛物线G上,把抛物线G绕着点P(t,-2)旋转180°,在1≤m≤3时,总有n随着m的增大而增大,请直接写出t的取值范围.

【答案】(1)-![]() ;(2)
;(2)![]() 或1;(3)当a>0时,t的取值范围是t≥2.5;当a<0时,t的取值范围是t≤1.5.
或1;(3)当a>0时,t的取值范围是t≥2.5;当a<0时,t的取值范围是t≤1.5.
【解析】
(1)首先利用配方法将抛物线的解析式变形为y=a(x-2)2-a-2,从而可得到抛物线的顶点坐标,然后依据顶点纵坐标为0可求得a的值;
(2)先求得A、B两点的坐标(用含a的式子表示),设直线l与抛物线G的对称轴x=2交于点D,则CD=a+3,①当0<a≤![]() 时,S△ABC=S△ADC-S△BCD;当a>
时,S△ABC=S△ADC-S△BCD;当a>![]() 时S△ABC=S△BCD-S△ACD,然后列出关于a的方程求解即可;
时S△ABC=S△BCD-S△ACD,然后列出关于a的方程求解即可;
(3)先求得抛物线G′的顶点坐标(用含t的式子表示),然后分为a>0和a<0两种情况时,最后,依据G′的增减性可得到关于t的不等式,从而可求得t的范围.
(1)y=ax2-4ax+3a-2=a(x-2)2-a-2.
∴顶点C的坐标为(2,-a-2).
∵顶点C在x轴上
∴-a-2=0,解得:a=-2.
(2)y=ax-2a+1与x、y轴分别交于A、B两点
∴A(![]() ,0),B(0,-2a+1),
,0),B(0,-2a+1),
设直线l与抛物线G的对称轴x=2交于点D,
直线x=2与x轴交于点H,则D(2,1),H(2,0),DC=1-(-a-2)=a+3.
①当0<a≤![]() 时,如图1所示:
时,如图1所示:
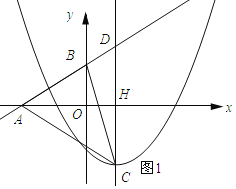
S△ABC=S△ADC-S△BCD.
∴![]() =2,解得:a=
=2,解得:a=![]() (负值已舍去)
(负值已舍去)
②当a>![]() 时,如图2所示:
时,如图2所示:
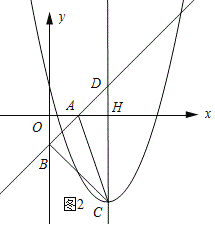
∵S△ABC=S△BCD-S△ACD=![]() CDOH-
CDOH-![]() CDAH=
CDAH=![]() CDAO,
CDAO,
∴![]() =2,
=2,
解得:a3=1,a4=-![]() (舍去负值)
(舍去负值)
综上所述:a的值为![]() 或1.
或1.
(3)解:y=ax2-4ax+3a-2=a(x-2)2-a-2.
∴抛物线的顶点坐标为(2,-a-2).
∵点P的坐标为(t,-2)
∴点P在直线y=-2上
依题意得:把抛物线G绕着点P(t,-2)旋转180°后,抛物线G的顶点在新抛物线G′上,且在1≤x≤3内,y随x的增大而增大,抛物线G与新抛物线G′的顶点关于P(t,-2)成中心对称,
∴G′的顶点坐标为(2t-2,a-2).
①若a>0,时,新抛物线G′的开口向下,
∴当2t-2≥3时,y随x的增大而增大,
∴t≥2.5.
②若a<0时,新抛物线G′开口向上,
∴当2t-2≤1时,y随x的增大而增大,
∴t≤1.5.
综上所述,当a>0时,t的取值范围是t≥2.5;当a<0时,t的取值范围是t≤1.5.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.