题目内容
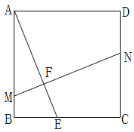
【题目】已知，正方形ABCD中，点E为BC边上任意一点（点E不与B，C重合），点F在线段AE上，过点F的直线
，分别交AB、CD于点M、N．
（1）如图，求证：
；
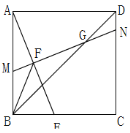
（2）如图，当点F为AE中点时，连接正方形的对角线BD，MN与BD交于点G，连接BF，求证：
；
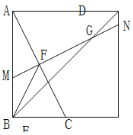
（3）如图，在（2）的条件下，若
，
，求BM的长度.
【答案】（1）见解析；（2）见解析；（3）
.
【解析】
（1）由正方形的性质得出∠B=90°，得出∠BAE+∠AEB=90°，由垂直的性质得出∠BAE+∠AMN=90°，即可得出结论；
（2）连接AG、EG、CG，证明△ABG≌△CBG得出AG=CG，∠GAB=∠GCB，证出EG=CG，由等腰三角形的性质得出∠GEC=∠GCE，证出∠AGE=90°，由直角三角形斜边上的中线性质得出BF=
AE，FG=AE，即可得出结论；
（3）过G作
交AD于点P，交BC于点Q，证明DP=PG=2，连接ME，证明MN是AE的垂直平分线，得
，
，再证明
得
，得
，进而得
，
中，由勾股定理得
，代入相关数据，从而得出结论.
（1）（1）证明：∵四边形ABCD是正方形，
∴∠B=90°，
∴∠BAE+∠AEB=90°，
∵MN⊥AE于F，
∴∠BAE+∠AMN=90°，
∴∠AEB=∠AMN；
（2）证明：连接AG、EG、CG，
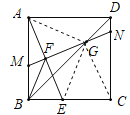
∵四边形ABCD是正方形，
∴AB=BC，∠ABG=∠CBG=45°，∠ABE=90°，
在△ABG和△CBG中，
，
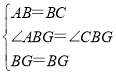∴△ABG≌△CBG（SAS），
∴AG=CG，∠GAB=∠GCB，
∵MN⊥AE于F，F为AE中点，
∴AG=EG，
∴EG=CG，
∴∠GEC=∠GCE，
∴∠GAB=∠GEC，
∵∠GEB+∠GEC=180°，
∴∠GEB+∠GAB=180°，
∵四边形ABEG的内角和为360°，∠ABE=90°，
∴∠AGE=90°，
在Rt△ABE和Rt△AGE中，AE为斜边，F为AE的中点，
∴BF=AE，FG=
AE，
∴BF=FG；
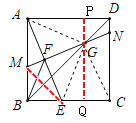
（3）过G作交AD于点P，交BC于点Q，则
，
，
中，
，
，
∴
，
∴
∵
，
∴
，
∴
即
连接ME ∵
于F，F为AE的中点,
∴MN是AE的垂直平分线
∴，
由（2）知
，
，
∴
，
又
，
∴
，
∴
，
∴
，
又
，
∴
∴
∴
∵
∴四边形PDCQ为矩形
∴
设
∵E是BC中点
∴
∴
∴
即
∴
∴
设
∴
中，由勾股定理得
∴
解得
∴
