题目内容

（1）证明：∵，    

∴．    …………………………………………（2分）

∵，      …………………………………………（1分）

∴∽．……………………………………… （1分）

∴． ……………………………………………（1分）

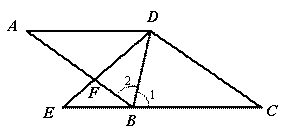
       （2）   ∵，

又∵，

  ∴．………………………………………………（1分）

∴．       ………………………………………………（1分）

又∵，

∴四边形是平行四边形 ………………………………………（1分）

∵，

∴．       ……………………………………………（1分）

∵平分，

∴．            …………………………………………（1分）

∴．

∴．        ……………………………………………（1分）

∴四边形是菱形．   ……………………………………………………（1分）

已知正方形ABCD的边长为4，E是CD上一个动点，以CE为一条直角边作等腰直角三角形CEF，连结BF、BD、FD．

（1）BD与CF的位置关系是                 ．

（2）①如图1，当CE=4（即点E与点D重合）时，△BDF的面积为          ．

②如图2，当CE=2（即点E为CD的中点）时，△BDF的面积为          ．

③如图3，当CE=3时，△BDF的面积为          ．

 


（3）如图4，根据上述计算的结果，当E是CD上任意一点时，请提出你对△BDF面积与正方形ABCD的面积之间关系的猜想，并证明你的猜想．

 


练习册系列答案
相关题目
22、如图，已知：点B，F，C，D在同一直线上，且FB=CD，AB∥ED，AC∥FE，请你根据上述条件，判断∠A与∠E的大小关系，并给出证明．
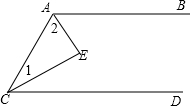精英家教网如图，AB∥CD，AE平分∠BAC，CE平分∠ACD，求∠E为多少？
下面是小明同学的解法，请帮助他完成证明．
证明：因为∠1=∠ECD=
1
2
∠ACD （原因：
 
）
又因为∠2=（∠BAE　　）=
1
2
∠CAB（原因：
 
）
又因为AB∥CD，
所以∠CAB+∠ACD=180°（原因：
 
）
所以∠1+∠2=
1
2
（∠CAB+∠ACD）=90°（等量代换）
又因为∠1+∠2+∠E=180°（原因：
 
）
所以∠E=90°．
对于正数x，规定f（x）=
x2
1+x2
，
（1）计算f（2）=
 
；f（
1
2
）=
 
；f（2）+f（
1
2
）=
 
；f（3）+f（
1
3
）=
 
；…
（2）猜想f（x）+f(
1
x
)=
 
，请予以证明．
（3）现在你会计算f(
1
2010
)+f（
1
2009
）+f（
1
2008
）+f（
1
2007
）+f（
1
2006
）+…f（
1
3
）+f（
1
2
）+f（1）+f（2）+f（3）+…+f（2006）+f（2007）+f（2008）+f（2009）+f（2010）的值了吗，写出你的计算过程．
如图，已知在Rt△ABC中，∠B=90°，AC=13，AB=5，O是AB上的点，以O为圆心，OB精英家教网为半径作⊙O．
（1）当OB=2.5时，⊙O交AC于点D，求CD的长；
（2）当OB=2.4时，AC与⊙O的位置关系如何？试证明你的结论．
20、如图，AE∥BC，AE平分∠CAD，试说明∠B=∠C
证明：∵AE∥BC
已知

∴∠1=
∠B（两直线平行，同位角相等）

∠2=
∠C（两直线平行，内错角相等）

又∵AE平分∠CAD
∴∠1=∠2
角平分线的定义

∴∠
B
=∠
C
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网