题目内容
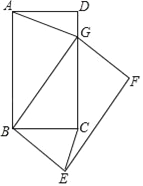
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)6
(3)6
【解析】试题分析:(1)、根据旋转图形的性质得出△ABG和△CBE相似,从而得出答案;(2)、本题分点G落在线段CD上和点G落DC的延长线上两种情况进行讨论,分别根据勾股定理求出AG的长度,然后根据△ABG和△CBE相似,从而得出CE的长度;(3)、当CE为⊙B的直径时,CE的值最大.
试题解析:(1)∵将矩形ABCD绕点B旋转得到矩形GBEF,
∴AB=BG,BC=BE,∠CBE=∠ABG, ∴![]() , ∴△ABG∽△CBE, ∴
, ∴△ABG∽△CBE, ∴![]() =
=![]() =
=![]() ;
;
(2)分两种情况讨论:①点G落在线段CD上时(如图1),
∵BG=AB=5,BC=3,CG=![]() =4, ∴DG=1,AG=
=4, ∴DG=1,AG=![]() =
=![]() ,
,
∵![]() =1,∠ABG=∠CBE, ∴△ABG∽△CBE, ∴
=1,∠ABG=∠CBE, ∴△ABG∽△CBE, ∴![]() =
=![]() ,
,
∴CE=![]() AG=
AG=![]() ×
×![]() =
=![]() ;
;
②点G落DC的延长线上时(如图2)
BG=5,BC=3,CG=4, ∴DG=9,AG=![]() =3
=3![]() , ∵
, ∵![]() =1,∠ABG=∠CBE,
=1,∠ABG=∠CBE,
∴△ABG∽△CBE, ∴![]() =
=![]() , ∴CE=
, ∴CE=![]() AG=
AG=![]() ×3
×3![]() =
=![]() ;
;


(3)在旋转的过程中,CE有最大值,
∵C、E在以点B为圆心,BC长为半径的圆上, ∴当CE为⊙B的直径时,CE的值最大,
即CE的最大值=2BC=6.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目




