Question

【题目】如图，抛物线C1：的顶点为A，与x轴的正半轴交于点B．

（1）将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍，求变换后得到的抛物线的解析式；

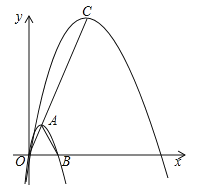
（2）将抛物线C1上的点（x，y）变为（kx，ky）（|k|＞1），变换后得到的抛物线记作C2，抛物线C2的顶点为C，点P在抛物线C2上，满足S△PAC=S△ABC，且∠APC=90°．

①当k＞1时，求k的值；

②当k＜﹣1时，请直接写出k的值，不必说明理由．

Answer 1

【答案】（1）；（2）①k=；②k=．

【解析】

试题分析：（1）由抛物线C1解析式求出A、B及原点坐标，将三点坐标都扩大到原来的2倍，待定系数求解可得；

（2）①如图1中，当k＞1时，与（1）同理可得抛物线C2的解析式为及顶点C的坐标，根据S△PAC=S△ABC知BP∥AC，继而可得△ABO是边长为2的正三角形，四边形CEBP是矩形，表示出点P的坐标，将其代入到抛物线C2解析式可求得k的值；

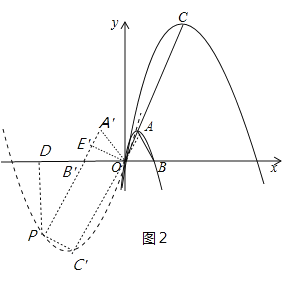
②如图2中，当k＜﹣1时，作△ABO关于y轴对称的△A′B′O，OE′⊥A′B′，同理可得四边形CEBP是矩形，先求出抛物线C2解析式，表示出点P的坐标，将其代入到抛物线C2解析式可求得k的值；

试题解析：（1）∵=，∴抛物线C1经过原点O，点A（1，）和点B（2，0）三点，∴变换后的抛物线经过原点O，（2，）和（4，0）三点，∴变换后抛物线的解析式为；

（2）①如图1中，当k＞1时，∵抛物线C2经过原点O，（k，k），（2k，0）三点，∴抛物线C2的解析式为，∴O、A、C三点共线，且顶点C为（k，k），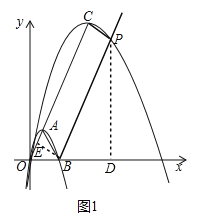

如图，∵S△PAC=S△ABC，∴BP∥AC，过点P作PD⊥x轴于D，过点B作BE⊥AO于E，由题意知△ABO是边长为2的正三角形，四边形CEBP是矩形，∴OE=1，CE=BP=2k﹣1，∵∠PBD=60°，∴BD=，PD=（2k﹣1），∴P（k+，（2k﹣1）），∴（2k﹣1）=，解得：k=；

②如图2中，当k＜﹣1时，∵抛物线C2经过原点O，（k，k），（2k，0）三点，∴抛物线C2的解析式为，∴O、A、C′三点共线，且顶点C′为（k，k），作△ABO关于y轴对称的△A′B′O，OE′⊥A′B′，∵S△PAC′=S△ABC=S△AC′B′，∴A′P∥AC′，由题意四边形PC′OE′是矩形，∴PE′=OC′=﹣2k，B′E′=1，PB′=﹣2k﹣1，在RT△PDB′中，∵∠PDB′=90°，∠PB′D=∠A′B′O=60°，∴DB′=PB′=，DP=（﹣2k﹣1），∴点P坐标[，（2k+1）]，∴（2k+1）=，∴k=．