题目内容
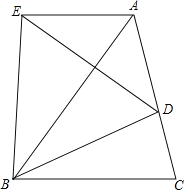
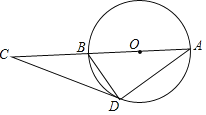
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (
(![]() )交于
)交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为6.
的横坐标为6.
(1)求![]() 的值;
的值;
(2)若双曲线![]() (
(![]() )上一点
)上一点![]() 的纵坐标为9,求
的纵坐标为9,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() (
(![]() )于
)于![]() ,
,![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点组成的四边形面积为96,求点
为顶点组成的四边形面积为96,求点![]() 的坐标.
的坐标.
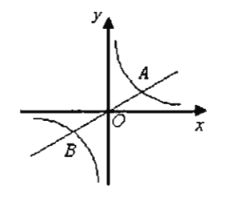
【答案】(1)18 ;(2)24;(3)![]() 或
或![]() ;
;
【解析】
(1)由条件可先求得A点坐标,代入反比例函数解析式可求得k的值;
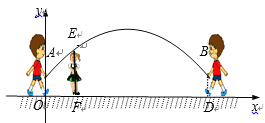
(2)首先求得C点的坐标,过C作x轴、y轴的垂线,垂足分别为D、E,过A作x轴的垂线,垂足为F,然后求出S矩形CDOE+S梯形CDFA,由反比例函数k的几何意义可求得S△COE和S△AOF,进而可求出S△AOC;
(3)设P点坐标为(m,![]() ),由反比例函数k的几何意义可得S△POM=S△AOD,然后根据正比例函数与反比例函数的对称性可得OA=OB,OP=OQ,然后根据S△POA=S梯形ADMP=
),由反比例函数k的几何意义可得S△POM=S△AOD,然后根据正比例函数与反比例函数的对称性可得OA=OB,OP=OQ,然后根据S△POA=S梯形ADMP=![]() S四边形APBQ构建方程即可解决问题.
S四边形APBQ构建方程即可解决问题.
解:(1)由点A在直线![]() 上,且点A的横坐标为6,代入可求得A点纵坐标为3,
上,且点A的横坐标为6,代入可求得A点纵坐标为3,
∴A点坐标为(6,3),
∵A点在双曲线![]() 上,
上,
∴k=6×3=18;
(2)当点C的纵坐标为9时,代入![]() 可得x=2,即C点坐标为(2,9),
可得x=2,即C点坐标为(2,9),
如图,过C作x轴、y轴的垂线,垂足分别为D、E,过A作x轴的垂线,垂足为F,
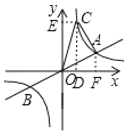
则OE=CD=9,OD=2,OF=6,AF=3,
∴DF=4,
∴S矩形CDOE+S梯形CDFA=![]() ,
,
又∵k=18,
∴S△COE=S△AOF=![]() ×18=9,
×18=9,
∴S△AOC=S矩形CDOE+S梯形CDFAS△COES△AOF=4299=24;
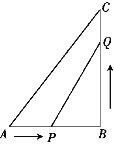
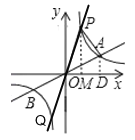
(3)设P点坐标为(m,![]() ),如图,作PM⊥x轴于M,
),如图,作PM⊥x轴于M,
∵P、A在双曲线上,
∴S△POM=S△AOD,
∴S△POA=S梯形ADMP=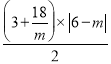 ,
,
由正比例函数与反比例函数关于原点对称可知,OA=OB,OP=OQ,
∴S△POA=![]() S四边形APBQ,即
S四边形APBQ,即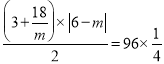 ,
,
解得m=2或18(负值已舍去),
∴P(2,9)或(18,1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.