题目内容
 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
分析:(1)利用勾股定理的逆定理得出△ABC是直角三角形,进而利用三角形面积得出CD的长,进而得出海港C是否受台风影响;
(2)利用勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间.
(2)利用勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间.
解答:解:(1)海港C受台风影响,
理由:过点C作CD⊥AB,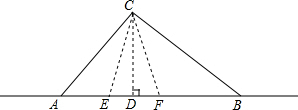
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED=
=70(km),
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时),
答:台风影响该海港持续的时间为7小时.
理由:过点C作CD⊥AB,

∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED=
| EC2-CD2 |
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时),
答:台风影响该海港持续的时间为7小时.
点评:本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 影响.
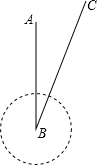
影响. 台风是一种自然灾害,如图,气象部门观测距A市正北方向200km的B处有一台风中心,其中心最大风力为12级,该台风中心正以18km/h的速度沿直线向C处移动,且台风中心风力不变,已知每远离台风中心20km,风力就减弱一级,若所受风力不到4级,则称不受台风影响,问:
台风是一种自然灾害,如图,气象部门观测距A市正北方向200km的B处有一台风中心,其中心最大风力为12级,该台风中心正以18km/h的速度沿直线向C处移动,且台风中心风力不变,已知每远离台风中心20km,风力就减弱一级,若所受风力不到4级,则称不受台风影响,问: 影响.试问:
影响.试问: