题目内容
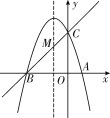
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1 上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标.
【答案】(1)y=-x2-2x+3,y=x+3;(2)M(-1,2).
【解析】
试题(1)根据题意得出关于a、b、c的方程组,求得a、b、c的值,即可得出抛物线的解析式,根据抛物线的对称性得出点B的坐标,再设出直线BC的解析式,把点B、C的坐标代入即可得出直线BC的解析式;
(2)点A关于对称轴的对称点为点B,连接BC,设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小,再求得点M的坐标.
试题解析:(1)依题意得: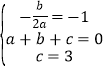 ,
,
解之得: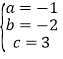 ,
,
∴抛物线解析式为y=-x2-2x+3,
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解得:![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2
∴M(-1,2).
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2).

练习册系列答案
相关题目