题目内容
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣1
(1)求抛物线的对称轴(用含m的式子去表示);
(2)若点(m﹣2,y1),(m,y2),(m+3,y3)都在抛物线y=x2﹣2mx+m2﹣1上,则y1、y2、y3的大小关系为 ;
(3)直线y=﹣x+b与x轴交于点A(3,0),与y轴交于点B,过点B作垂直于y轴的直线l与抛物线y=x2﹣2mx+m2﹣1有两个交点,在抛物线对称轴右侧的点记为P,当△OAP为钝角三角形时,求m的取值范围.
【答案】(1)x![]() m;(2)y2>y3>y1;(3)m<5.
m;(2)y2>y3>y1;(3)m<5.
【解析】
(1)函数的对称轴为:x![]() m;
m;
(2)函数对称轴为x=m,函数开口向上,x=m时函数取得最小值,即可求解;
(3)分∠OPA是钝角、∠OAP是钝角两种情况,分别求解即可.
解:(1)函数的对称轴为:x![]() m;
m;
(2)函数对称轴为x=m,函数开口向上,x=m时函数取得最小值,
故:y2>y3>y1;
(3)把点A的坐标代入y=﹣x+b的表达式并解得:b=3,
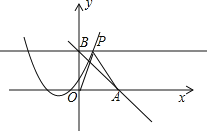
则点B(0,3),直线表达式为:y=﹣x+3,
当y=3时,y=x2﹣2mx+m2﹣1=3,
则x=m±2,则点P(m﹣2,3),
则OP2=(m﹣2)2+9,OA2=9,PA2=(m﹣5)2+9,
①当∠OPA是钝角时,
则OP2+PA2>OA2,
即:(m﹣2)2+9+(m﹣5)2+9>9,
解得:m为任意实数;
②当∠OAP是钝角时,
OA2+PA2>OP2,
即9+(m﹣5)2+9>(m﹣2)2+9
解得:m<5.
即:m的取值范围为:m<5.

【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.