题目内容
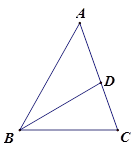
在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻拆,点B落在点E处,设PE交AC于F,连接CD

(1)求证:△PCF的周长= CD;
CD;
(2)设DE交AC于G,若 ,CD=6,求FG的长
,CD=6,求FG的长

(1)求证:△PCF的周长=
 CD;
CD;(2)设DE交AC于G,若
 ,CD=6,求FG的长
,CD=6,求FG的长(1)证明见解析;(2)FG的长为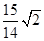 .
.
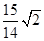 .
.试题分析:.(1)连接CE,根据三角形的角边关系可以得到∠FCE=∠FEC,从而FC=FE,△PCF的周长=
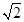 CD;
CD;(2) 由.(1)结论CP+PF+CF=
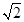 CD,和
CD,和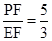 ,CD=6,求出CF=EF=
,CD=6,求出CF=EF=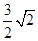 ,作GK⊥EF于点K,易得FG的长为
,作GK⊥EF于点K,易得FG的长为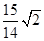 .
.试题解析:.(1)连接CE,
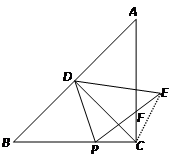
∵CA=CB,D为AB中点,
∴∠BCD=∠ACD=45°,
由翻折可知∠B=∠DEP=45°,
∴∠DCF=∠DEF=45°,
CD=BD=DE,
∴∠DCE=∠DEC,
∴∠DCE-∠DCA=∠DEC-∠DEF,
即∠FCE=∠FEC,
∴FC=FE,
∴CF+PF=PE=BP,
∴CP+PF+CF=BC=
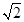 CD,
CD,∴△PCF的周长=
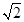 CD;
CD;(2)∵
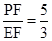 ,
,∴设PF=5x,EF=CF=3x,
在Rt△FCP中,PF2=CP2+CF2,
∴CP=4x,
∵CP+PF+CF=
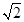 CD,
CD,∴4x+5x+3x=6
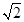 ,
,x=
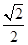 ,
,CF=EF=3x=
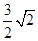 ,
,作GK⊥EF于点K,
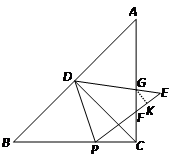
∵tan∠GFE=tan∠PFC=
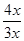 =
=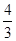 ,
,设GK=4a,FK=3a,EK=4a,
∴EF=7a=
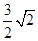 ,
,a=
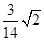 ,
,FG=5a=
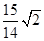 ,
,∴FG的长为
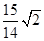 .
.
练习册系列答案
相关题目
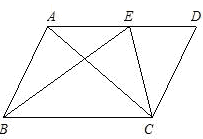
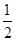 ∠BAD.
∠BAD.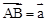 ,
,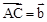 ,那么
,那么 .
.