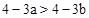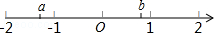题目内容
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写下表(单位:元)
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少?
(1)根据题题意,填写下表(单位:元)
| 累计购物实际花费 | 130 | 290 | … | x |
| 在甲商场 | 127 | | … | |
| 在乙商场 | 126 | | … | |
(3)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少?
解:(1)填表如下:
(2)根据题意得:0.9x+10=0.95x+2.5,
解得:x=150。
答:当x=150时,小红在甲、乙两商场的实际花费相同。
(3)由0.9x+10<0.95x+2.5解得:x>150,
由0.9x+10>0.95x+2.5,解得:x<150,
∴当小红累计购物大于150时上没封顶,选择甲商场实际花费少;
当小红累计购物超过100元而不到150元时,在乙商场实际花费少。
| 累计购物实际花费 | 130 | 290 | … | x |
| 在甲商场 | 127 | 271 | … | 0.9x+10 |
| 在乙商场 | 126 | 278 | … | 0.95x+2.5 |
解得:x=150。
答:当x=150时,小红在甲、乙两商场的实际花费相同。
(3)由0.9x+10<0.95x+2.5解得:x>150,
由0.9x+10>0.95x+2.5,解得:x<150,
∴当小红累计购物大于150时上没封顶,选择甲商场实际花费少;
当小红累计购物超过100元而不到150元时,在乙商场实际花费少。
试题分析:(1)根据已知得出:
在甲商场:100+(290-100)×0.9=271,100+(290-100)×0.9x=0.9x+10;
在乙商场:50+(290-50)×0.95=278,50+(290-50)×0.95x=0.95x+2.5。
(2)根据题中已知条件,求出0.95x+2.5,0.9x+10相等,从而得出正确结论。
(3)根据0.95x+2.5与0.9x+10相比较,从而得出正确结论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,并在数轴上表示解集.
,并在数轴上表示解集.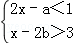 的解集为﹣1<x<1,那么(a+1)(b﹣1)的值等于 _________ .
的解集为﹣1<x<1,那么(a+1)(b﹣1)的值等于 _________ .




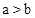 ,则下列不等式变形错误的是【 】
,则下列不等式变形错误的是【 】