题目内容
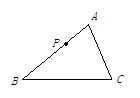
如图,△ABC中,三边互不相等,点P是AB上一点,有过点P的直线将△ABC切出一个小三角形与△ABC相似,这样的直线一共有
- A.5条
- B.4条
- C.3条
- D.2条
B
试题分析:首先,要确立两个三角形相似,即其中两组角应该对应相等。过点P做直线PO∥AC,此时两个三角形相似;过点P做直线PO,其中O在BC上,令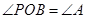 ,此时两个三角形相似;过点P做直线PO∥BC,此时两个三角形相似;过点P做直线PO,O在AC上,令
,此时两个三角形相似;过点P做直线PO∥BC,此时两个三角形相似;过点P做直线PO,O在AC上,令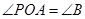 ,此时两个三角形相似。
,此时两个三角形相似。
考点:相似三角形的判定
点评:此题考查的是相似三角形的判定,两个三角形相似,即其中两组角应该对应相等,由于P点确立,即两个三角形肯定有一组公共角,此时只要令另外一组角相等,两个三角形必定相似。
试题分析:首先,要确立两个三角形相似,即其中两组角应该对应相等。过点P做直线PO∥AC,此时两个三角形相似;过点P做直线PO,其中O在BC上,令
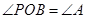 ,此时两个三角形相似;过点P做直线PO∥BC,此时两个三角形相似;过点P做直线PO,O在AC上,令
,此时两个三角形相似;过点P做直线PO∥BC,此时两个三角形相似;过点P做直线PO,O在AC上,令 ,此时两个三角形相似。
,此时两个三角形相似。考点:相似三角形的判定
点评:此题考查的是相似三角形的判定,两个三角形相似,即其中两组角应该对应相等,由于P点确立,即两个三角形肯定有一组公共角,此时只要令另外一组角相等,两个三角形必定相似。

练习册系列答案
相关题目
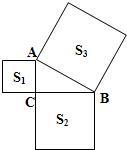 13、如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=36,S3=100,则S2=
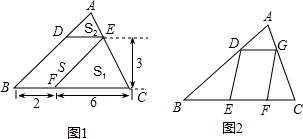
13、如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=36,S3=100,则S2=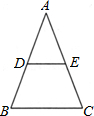 如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )
如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )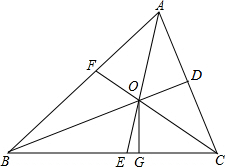 如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,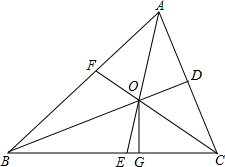 如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G, ∠BAC之间的数量关系,并说明理由;
∠BAC之间的数量关系,并说明理由;