题目内容
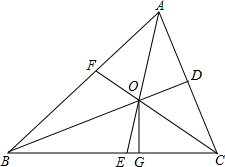 如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
(1)猜想∠BOC与90°+ ∠BAC之间的数量关系,并说明理由;
∠BAC之间的数量关系,并说明理由;
(2)∠BOE与∠COG相等吗?为什么?
解:(1)∠BOC=90°+ ∠BAC;
∠BAC;
理由:∵△ABC中,三条角平分线AE、BD、CF相交于点O,
∴∠OBC= ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,
∵∠ABC+∠ACB=180°-∠BAC,
∴∠BOC=180°-(∠OBC+∠OCB)=180°- (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠BAC)=90°+
(180°-∠BAC)=90°+ ∠BAC;
∠BAC;
(2)∠BOE=∠COG
理由:由(1)知∠AOB=90°+ ∠ACB,
∠ACB,
∴∠BOE=180°-∠AOB=180°-(90°+ ∠ACB)=90°-
∠ACB)=90°- ∠ACB,
∠ACB,
又∵OC平分∠ACB,OG⊥BC,
∴∠COG=90°- ∠ACB,
∠ACB,
∴∠BOE=∠COG.
分析:(1)由△ABC中,三条角平分线AE、BD、CF相交于点O,可得∠OBC= ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,继而可得∠BOC=180°-(∠OBC+∠OCB)=180°-
∠ACB,继而可得∠BOC=180°-(∠OBC+∠OCB)=180°- (∠ABC+∠ACB),则可证得结论;
(∠ABC+∠ACB),则可证得结论;
(2)由(1)知∠AOB=90°+ ∠ACB,则可得∠BOE=90°-
∠ACB,则可得∠BOE=90°- ∠ACB,又由OC平分∠ACB,OG⊥BC,即可得∠COG=90°-
∠ACB,又由OC平分∠ACB,OG⊥BC,即可得∠COG=90°- ∠ACB,则可证得∠BOE=∠COG.
∠ACB,则可证得∠BOE=∠COG.
点评:此题考查了三角形内角和定理以及角平分线的定义.此题难度适中,注意掌握整体思想与数形结合思想的应用.
 ∠BAC;
∠BAC; 理由:∵△ABC中,三条角平分线AE、BD、CF相交于点O,
∴∠OBC=
 ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,∵∠ABC+∠ACB=180°-∠BAC,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
 (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠BAC)=90°+
(180°-∠BAC)=90°+ ∠BAC;
∠BAC;(2)∠BOE=∠COG
理由:由(1)知∠AOB=90°+
 ∠ACB,
∠ACB,∴∠BOE=180°-∠AOB=180°-(90°+
 ∠ACB)=90°-
∠ACB)=90°- ∠ACB,
∠ACB,又∵OC平分∠ACB,OG⊥BC,
∴∠COG=90°-
 ∠ACB,
∠ACB,∴∠BOE=∠COG.
分析:(1)由△ABC中,三条角平分线AE、BD、CF相交于点O,可得∠OBC=
 ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,继而可得∠BOC=180°-(∠OBC+∠OCB)=180°-
∠ACB,继而可得∠BOC=180°-(∠OBC+∠OCB)=180°- (∠ABC+∠ACB),则可证得结论;
(∠ABC+∠ACB),则可证得结论;(2)由(1)知∠AOB=90°+
 ∠ACB,则可得∠BOE=90°-
∠ACB,则可得∠BOE=90°- ∠ACB,又由OC平分∠ACB,OG⊥BC,即可得∠COG=90°-
∠ACB,又由OC平分∠ACB,OG⊥BC,即可得∠COG=90°- ∠ACB,则可证得∠BOE=∠COG.
∠ACB,则可证得∠BOE=∠COG.点评:此题考查了三角形内角和定理以及角平分线的定义.此题难度适中,注意掌握整体思想与数形结合思想的应用.

练习册系列答案
相关题目
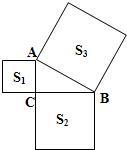 13、如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=36,S3=100,则S2=
13、如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=36,S3=100,则S2=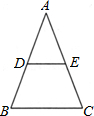 如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )
如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )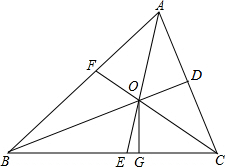 如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
如图,△ABC中,三条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,