题目内容
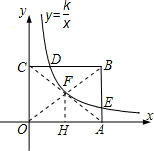
如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数 y=
y= 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)若矩形OABC对角线的交点为F,请判断点F是否在此反比例函数的图象上,并说明理由.
(3)若AD与BO的交点为Q,请判断点Q是否在此反比例函数的图象上,并说明理由.
 解:(1)把D(1,3)代入y=
解:(1)把D(1,3)代入y= ,得3=
,得3=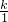 ,
,∴k=3.
∴y=
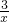 .
.∴当x=4时,y=
 ,
,∴E(4,
 ).
).(2)点F在反比例函数的图象上.
理由如下:
连接AC,OB交于点F,过F作FH⊥x轴于H.
∵四边形OABC是矩形,
∴OF=FB=
 OB.
OB.又∵∠FHO=∠BAO=90°,∠FOH=∠BOA,
∴△OFH∽△OBA.
∴
 =
=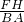 =
=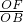 =
= ,
,∴OH=2,FH=
 .
.∴F(2,
 ).
).即当x=2时,y=
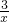 =
= ,
,∴点F在反比例函数y=
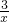 的图象上.
的图象上.(3)直线OB与AD所在直线分别为:
y=kx,图象过(4,3)点,∴y=
 x,
x,y=ax+b.过点(4,0),(1,3),
∴
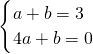 ,
,解得:
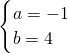 ,
,∴y=-x+4,
 ,
,解得:x=
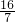 ,y=
,y= ,
,代入解析式:
当x=
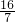 时,y=
时,y=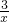 =
=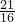 ,
,∴(
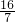 ,
, )不在此反比例函数的图象上.
)不在此反比例函数的图象上.分析:(1)把已知点代入反比例函数的解析式,求出其解析式;再进一步把x=4代入,从而求出E点的坐标.
(2)利用矩形及相似三角形的性质,判断出F点与反比例函数图象的关系.
(3)分别求直线BO与AD解析式,求出交点即可.
点评:此题主要考查了反比例函数的综合应用,此题比较复杂,把反比例函数y=
 的图象、矩形的性质及相似三角形的性质相结合,考查了学生对所学知识的综合运用能力.
的图象、矩形的性质及相似三角形的性质相结合,考查了学生对所学知识的综合运用能力. 
练习册系列答案
相关题目
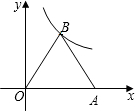 如图,已知:正△OAB的面积为
如图,已知:正△OAB的面积为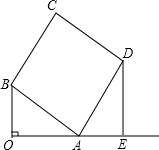 长线交于点E.
长线交于点E.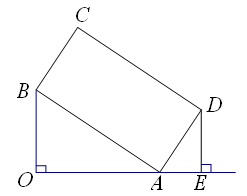
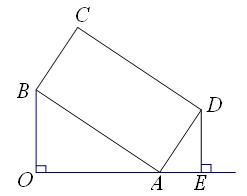
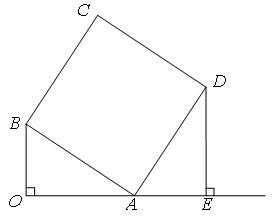
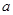 ,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;
,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;