Question

【题目】四边形是菱形，，

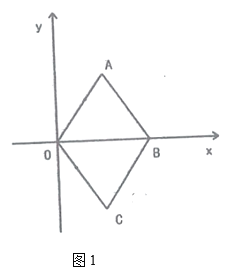
（1）如图1，作的平分线，交于（不写作法和证明，保留作图痕迹）

（2）在（1）的条件下，点在直线上，最大值时，求的长

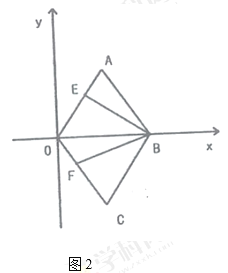
（3）如图2，，分别是线段，上的动点，，求四边形周长的最小值.

Answer 1

【答案】（1）见解析（2）；（3）

【解析】

（1）根据角平分线尺规作图的方法作图即可；

（2）先在直线OP上任取一点P，根据OD是AB的垂直平分线，根据PA=PB得出PC－PB<BC，得出当P、B、C三点共线的时候最大，结合等腰三角形三线合一以及三角函数即可求出OP的长

（3）先证明△ABE≌△OBF，得到AE=OF，可得四边形周长等于2BE+OA，可得出当BE最短时，四边形周长最小，再根据垂线段最短，可得当BE垂直AO时，BE最短，再根据三角函数求出此时BE的长

解：（1）作图如下：

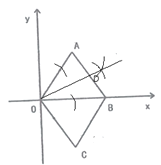
（2）如图：在直线OD上任取一点P，连接PA、PB、PC

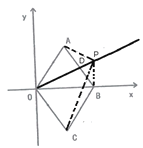
∵是菱形，

∴∠OAB=60°，∠AOB=120°

∴；

∴△AOB为等边三角形

∵OD平分∠AOB

∴OD⊥AB，且D为AB中点；

∴OD为AB的垂直平分线

∴PA=PB

∴

∴当P、B、C三点共线时，有最大值，即有最大值

如下图，延长CB交OD于P，点即为所求

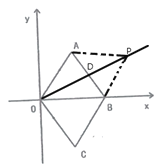
∵∠OBC=60°

∴∠OBP=120°

又∵∠DOB=30°

∴∠OPD=30°

∴OB=PB

∵OD⊥AB

∴D为OP中点

在Rt△OBD中，OB=6，∠DOB=30°

∴

∴OP=2OD=

即：当OP=时，有最大值

（3）如图，连接EF

∵由（1）知△AOB为等边三角形

∴∠ABO=∠ABE+∠EBO=60°

∵∠EBF=∠OBF+∠EBO=60°

∴∠ABE=∠OBF

在△ABE与△OBF中

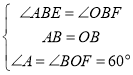
∴△ABE≌△OBF（ASA）

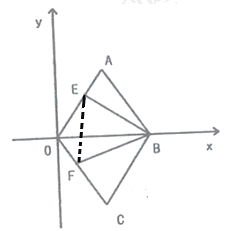
∴BE=BF，AE=OF

∵四边形周长=BE+BF+OF+OE=2BE+AE+OE=2BE+OA

∵OA=OB=6

∴四边形周长=2BE+6

∴当BE最小时，四边形周长最小

∴当BE⊥OA时，BE最短

在Rt△ABE中，∠A=60°，AB=6

∴

∴四边形周长最小值是

故答案为：