题目内容
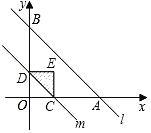
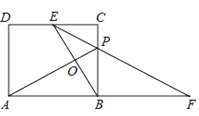
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
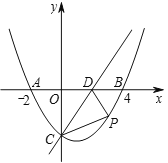
【答案】(1)![]() ;(2)P(3,﹣
;(2)P(3,﹣![]() );(3)点E的坐标为(﹣2,2
);(3)点E的坐标为(﹣2,2![]() )或(﹣2,﹣2
)或(﹣2,﹣2![]() ).
).
【解析】
(1)用交点式函数表达式得:y=a(x+2)(x-4)=a(x2-2x-8),即可求解;
(2)由S△PCD=S△PDO+S△PCO-S△OCD,即可求解;
(3)如图,经过点O、B的圆F与直线l相切于点E,此时,sin∠BEO最大,即可求解.
解:(1)用交点式函数表达式得:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
即﹣8a=﹣3,解得:a=![]() ,
,
则函数的表达式为:![]() ;
;
(2)y=![]() x﹣3,令y=0,则x=2,即点D(2,0),
x﹣3,令y=0,则x=2,即点D(2,0),
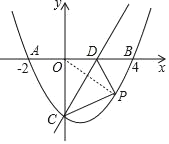
连接OP,设点P(x,![]() ),
),
S△PCD=S△PDO+S△PCO﹣S△OCD
=![]() ,
,
∵﹣![]() <0,∴S△PCD有最大值,
<0,∴S△PCD有最大值,
此时点P(3,﹣![]() );
);
(3)如图,经过点O、B的圆F与直线l相切于点E,此时,sin∠BEO最大,
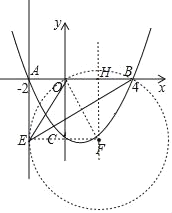
过圆心F作HF⊥x轴于点H,则OH=![]() OB=2=OA,OF=EF=4,
OB=2=OA,OF=EF=4,
∴HF=2![]() ,过点E的坐标为(﹣2,﹣2
,过点E的坐标为(﹣2,﹣2![]() );
);
同样当点E在x轴的上方时,其坐标为(﹣2,2![]() );
);
故点E的坐标为(﹣2,2![]() )或(﹣2,﹣2
)或(﹣2,﹣2![]() ).
).

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
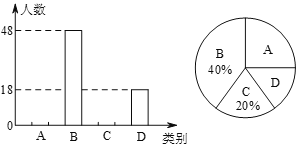
全优测试卷系列答案【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.