题目内容
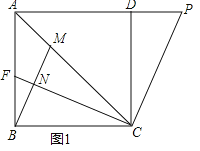
【题目】如图1,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,过点C作CF⊥CP交于C,交AB于点F,过点B作BM⊥CF于点N,交AC于点M.
(1)若AP=![]() AC,BC=4,求S△ACP;
AC,BC=4,求S△ACP;
(2)若CP﹣BM=2FN,求证:BC=MC;
【答案】(1)S△ACP=7![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)由正方形的性质得出AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,由勾股定理求出AC,得出AP,即可求出S△ACP;(2)在CF上截取NG=FN,连接BG,则CF-CG=2FN,证出∠BCF=∠DCP,由ASA证明△BCF≌△DCP,得出CF=CP,证出CG=BM,由SAS证明△ABM≌△BCG,得出∠AMB=∠BGC,因此∠BMC=∠BGF,由线段垂直平分线的性质得出BF=BG,得出∠BFG=∠BGF,因此∠BMC=∠CBM,即可得出结论
试题解析:(1)∵四边形ABC是正方形,
∴AD∥BC,AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,
∴AC=![]() ,
,
∴AP=![]() AC=
AC=![]() ×
×![]() =
=![]() ,
,
∴S△ACP=![]() AP×CD=
AP×CD=![]() ×
×![]() ×4=7
×4=7![]() ;
;
(2)证明:在CF上截取NG=FN,连接BG,如图1所示:
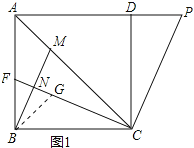
则CF﹣CG=2FN,
∵CF⊥CP,
∴∠PCF=90°,
∴∠BCF=∠DCP,
在△BCF和△DCP中, 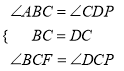 ,
,
∴△BCF≌△DCP(ASA),
∴CF=CP,
∵CP﹣BM=2FN,
∴CG=BM,
∵∠ABC=90°,BM⊥CF,
∴∠ABM=∠BCG,∠BFG=∠CBM,
在△ABM和△BCG中, 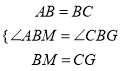 ,
,
∴△ABM≌△BCG(SAS),
∴∠AMB=∠BGC,
∴∠BMC=∠BGF,
∵GN=FN,BM⊥CF,
∴BF=BG,
∴∠BFG=∠BGF,
∴∠BMC=∠CBM,
∴BC=MC.