题目内容
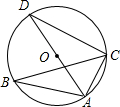已知：如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=30°，则∠CAD等于
- A.30°
- B.40°
- C.50°
- D.60°
D
分析：根据圆周角定理可知∠B=∠D=30°，∠ACD=90°，在Rt△ACD中，已知了∠D的度数，易求出∠CAD的度数．
解答：∵AD是⊙O的直径
∴∠ACD=90°
由圆周角定理知，∠D=∠B=30°
∴∠CAD=90°-∠D=60°．
故选D．
点评：本题利用了圆周角定理、直角三角形的性质求解．
分析：根据圆周角定理可知∠B=∠D=30°，∠ACD=90°，在Rt△ACD中，已知了∠D的度数，易求出∠CAD的度数．
解答：∵AD是⊙O的直径
∴∠ACD=90°
由圆周角定理知，∠D=∠B=30°
∴∠CAD=90°-∠D=60°．
故选D．
点评：本题利用了圆周角定理、直角三角形的性质求解．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
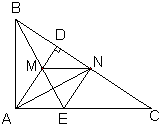17、已知，如图，△ABC中，∠BAC=90°，AD⊥BC于点D，BE平分∠ABC，交AD于点M，AN平分∠DAC，交BC于点N．
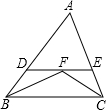已知：如图，∠ABC、∠ACB 的平分线相交于点F，过F作DE∥BC于D，交AC 于E，且AB=6，AC=5，求三角形ADE的周长．
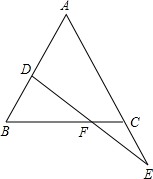已知：如图，△ABC是等边三角形，点D在AB上，点E在AC的延长线上，且BD=CE，DE交BC于F，求证：BF=CF+CE．
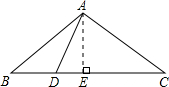已知：如图，△ABC中，AB=AC=10，BC=16，点D在BC上，DA⊥CA于A．
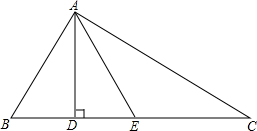已知：如图，△ABC中，AD⊥BC，BD=DE，点E在AC的垂直平分线上．