��Ŀ����
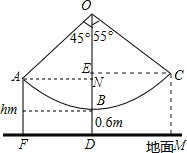
����Ŀ��ij��ũ����������һ����ǧ��������ͼ��ʾ����ǧ����OB�ij�Ϊ3m����ֹʱ��̤�嵽�������BD�ij�Ϊ0.6m��̤���Ⱥ��Բ��ƣ���Ϊ��ȫ��������������涨����ͯ������ȫ�߶���Ϊhm�����˵�����ȫ�߶���Ϊ2m����������ȷ��0.1m��
��1��������OA��OB��45���н�ʱ��ǡΪ��ͯ�İ�ȫ�߶ȣ���h���� ��m
��2��ij����������ǧʱ������OC��OB�����н�Ϊ55�����ʴ����Ƿ�ȫ�����ο����ݣ�![]() ��1.41��sin55���0.82��cos55���0.57��tan55���1.43��
��1.41��sin55���0.82��cos55���0.57��tan55���1.43��

���𰸡���1��1.5����2�������ǰ�ȫ�ģ�
��������
��1���������Ҷ��������OE���ٸ���AF=OB+BD�����DE�����ɵó�h��ֵ��
��2����C����CM��DF����DF�ڵ�M��������֪���������Ҷ������OE���ٸ���CM=OB+DE-OE�����CM��������˵�����ȫ�߶������бȽϣ����ɵó��𰸣�
�⣺��1����Rt��ANO�У���ANO��90����
��cos��AON��![]() ��
��
��ON��OAcos��AON��
��OA��OB��3m����AON��45����
��ON��3cos45���2.12m��
��ND��3+0.6��2.12��1.5m��
��h��ND��AF��1.5m��
�ʴ�Ϊ1.5��
��2����ͼ����C����CM��DF����DF�ڵ�M��
��Rt��CEO����CEO��90����
��cos��COE��![]() ��
��
��OE��OCcos��COF��
��OB��OC��3m����CON��55����
��OE��3cos55���1.72m��
��ED��3+0.6��1.72��1.9m��
��CM��ED��1.9m��
�߳��˵�����ȫ�߶���Ϊ2m��
������ǰ�ȫ�ģ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��2019��5�£������������Ի���ᡱ�ڱ����ɹ��ٰ죬ij�о�����Ϊ���˽�10-60�������������Ա��δ��Ĺ�ע�̶ȣ����ѡȡ��100�������ڸ÷�Χ�ڵ���������˵��飬�����Ѽ����������Ƴ����в�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������ʾ��
��� | ����� | Ƶ���������� |
��һ�� |
| 5 |
�ڶ��� |
|
|
������ |
| 35 |
������ |
| 20 |
������ |
| 15 |
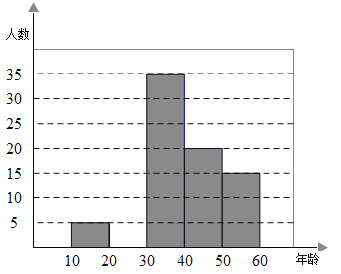

��ֱ��д����3������������ͳ��ͼ������Ӧ��Բ�Ľ���_________�ȣ������������10-60�������300���ˣ���40-50������εĹ�ע���δ�������Լ��___________���ˣ�
����Ŀ��Ϊ�����ͼ����Ǹ������ҵ�����ijɱ�ѹ����ij�е�������˼ۣ��������������б���ͼ������![]() ��
��![]() ��
��![]() ��������
��������
��ʻ·�� | �շѱ� | |
����ǰ | ���ۺ� | |
������ | ��9Ԫ | �� |
���� | ÿ����2Ԫ | ÿ���� |
���� | ÿ���� | |
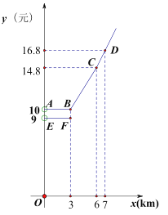
����ʻ·��Ϊ![]() ʱ������ǰ���˼�Ϊ
ʱ������ǰ���˼�Ϊ![]() ��Ԫ�������ۺ���˼�Ϊ
��Ԫ�������ۺ���˼�Ϊ![]() ��Ԫ������ͼ������
��Ԫ������ͼ������![]() ��ʾ
��ʾ![]() ��
��![]() ֮��ĺ�����ϵ���߶�
֮��ĺ�����ϵ���߶�![]() ��ʾ
��ʾ![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵ������ͼ����Ϣ��������и��⣺
֮��ĺ�����ϵ������ͼ����Ϣ��������и��⣺
��1����գ�![]() _____��
_____��![]() _____��
_____��![]() _______��
_______��
��2��д����![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��������ͼ�л����ú���ͼ��
֮��ĺ�����ϵʽ��������ͼ�л����ú���ͼ��
��3������ʻ·��Ϊ![]() ʱ�����۵���ǰ���˼۵ĸߵͣ�
ʱ�����۵���ǰ���˼۵ĸߵͣ�