题目内容
(2012•建邺区一模)如图,在△ABC中,AB=AC=10,BC=16,M为BC的中点.⊙A的半径为3,动点O 从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.
从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.
(1)当以OB为半径的⊙O与⊙A相切时,求t的值;
(2)探究:在线段BC上是否存在点O,使得⊙O与直线AM相切,且与⊙A相外切?若存在,求出此时t的值及相应的⊙O的半径;若不存在,请说明理由.
 从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.
从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.(1)当以OB为半径的⊙O与⊙A相切时,求t的值;
(2)探究:在线段BC上是否存在点O,使得⊙O与直线AM相切,且与⊙A相外切?若存在,求出此时t的值及相应的⊙O的半径;若不存在,请说明理由.
分析:(1)在△ABC中,根据AB=AC,M为BC中点得到AM⊥BC,在Rt△ABM中,AB=10,BM=8得到AM=6.然后分当⊙O与⊙A相外切与当⊙O与⊙A相内切两种情况求得t值即可;
(2)分当点O在BM上运动时(0<t≤8)和当点O在MC上运动时(8<t≤16)两种情况求得t值即可.
(2)分当点O在BM上运动时(0<t≤8)和当点O在MC上运动时(8<t≤16)两种情况求得t值即可.
解答:解:(1)在△ABC中,∵AB=AC,M为BC中点
∴AM⊥BC
在Rt△ABM中,AB=10,BM=8∴AM=6.(1分)
当⊙O与⊙A相外切
可得 (t+3)2=(8-t)2+62解得t=
(3分)
当⊙O与⊙A相内切
可得(t-3)2=(t-8)2+62解得t=
(5分)
∴当t=
或t=
时,⊙O与⊙A相切.
(2)存在
当点O在BM上运动时(0<t≤8))
可得(8-t)2+62=(8-t+3)2解得t=
(8分)
此时半径r=
当点O在MC上运动时(8<t≤16))
可得(t-8)2+62=(t-8+3)2解得t=
(10分)
此时半径r=
当t=
或t=
时,r=
,⊙O与直线AM相切并且与⊙A相外切.
∴AM⊥BC
在Rt△ABM中,AB=10,BM=8∴AM=6.(1分)
当⊙O与⊙A相外切
可得 (t+3)2=(8-t)2+62解得t=
| 91 |
| 22 |
当⊙O与⊙A相内切
可得(t-3)2=(t-8)2+62解得t=
| 91 |
| 10 |
∴当t=
| 91 |
| 22 |
| 91 |
| 10 |
(2)存在
当点O在BM上运动时(0<t≤8))
可得(8-t)2+62=(8-t+3)2解得t=
| 7 |
| 2 |
此时半径r=
| 9 |
| 2 |
当点O在MC上运动时(8<t≤16))
可得(t-8)2+62=(t-8+3)2解得t=
| 25 |
| 2 |
此时半径r=
| 9 |
| 2 |
当t=
| 7 |
| 2 |
| 25 |
| 2 |
| 9 |
| 2 |
点评:本题考查了圆与圆的位置关系及勾股定理、切线的性质等知识,考查的知识点比较多,难度较大.

练习册系列答案
相关题目
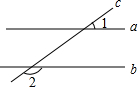 (2012•建邺区一模)如图,直线a、b被第三条直线c所截,且a∥b,若∠1=35°,则∠2=
(2012•建邺区一模)如图,直线a、b被第三条直线c所截,且a∥b,若∠1=35°,则∠2=
 (2012•建邺区一模)如图,矩形ABCD中,A(-4,1),B(0,1),C(0,3),则D点坐标是
(2012•建邺区一模)如图,矩形ABCD中,A(-4,1),B(0,1),C(0,3),则D点坐标是