��Ŀ����
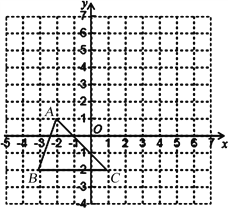
����Ŀ����ͼ1��һ����ֱ�Ĺ�·����A��B��C���أ�B��C�������150ǧ�ף��ס������������ֱ�
��B��C����ͬʱ�������ع�·ʼ������������У��ֱ�ʻ��C��B����. �ס���������A�صľ���y1��y2��ǧ�ף�����ʻʱ��x��ʱ���Ĺ�ϵ��ͼ2��ʾ��
��1������ͼ1�б��A�ص�λ�ã���д����Ӧ�ľ��룺AB= km��AC= km��
��2����ͼ2������׳�����C�ص�ʱ��a�����ֱ�д���׳�����A��֮ǰy1����ʻʱ��x�Ĺ�ϵʽ�ͼ׳���A���뿪��C�ص�y1����ʻʱ��x�Ĺ�ϵʽ(����Ҫд�Ա�����ȡֵ��Χ)��
��3���ס������������жԽ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ���������������öԽ���ͨ����ʱ�乲�ж��


���𰸡���1��60��90����2����B��A�� ![]() ����A��C��
����A��C�� ![]() ����3��
����3��![]()
�������������������1����ͼ�ڵã�AB=60km����AC=90km����AB��AC=2��3���ݴ˻�ͼ��
��2�����ݣ�1��0������0��60����y1����ʻʱ��x�ĺ�����ϵʽ��������ٶ�Ϊ60km/h��
�����������ȫ�̵�ʱ��Ϊ��150��60=2.5�����ݣ�1��0������2.5��90�����߶Σ�
��3���ֱ���DM��MC��BC�Ľ���ʽ������������A��С�ڵ���15kmʱ��Ӧ��ʱ�䣬������ʱ���ɣ�
���������(1)

��ͼ�٣�����AB:AC=2:3����AB=60km����AC=90km��

(2)��0<x<1.2ʱ,��AB�Ľ���ʽΪ��y1=kx+b��
��(1,0)��(0,60)����ã� ![]() ��
��
��ã� ![]() ��
��
��y1=60x+60��
���ٶ�Ϊ��60��1=60��
��150��60=2.5��
��ͼ����ʾ������׳�����C�صĺ���ͼ��
ͬ��BC�Ľ���ʽΪ��y1=60x60��
(3)DM�Ľ���ʽΪ��y2=75x+90��
ME�Ľ���ʽΪ��y2=75x90��
������ã� ![]() ��
��
��ã�34x54��
������ã� ![]() ��
��
��ã�1x75��
��1x54��
541=14��
����������ͬʱ��ָ�������öԽ���ͨ����ʱ��14Сʱ=15���ӡ�

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�