题目内容
我市某镇组织20辆汽车装运完A、B、C三种水果共100吨到外地销售,按计划,20辆车都要装运,每辆汽车只能装运同一种水果,且必须装满,根据下表提供的信息,解答以下问题.| 水果品种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨水果获得利润(百元) | a | 16 | 10 |
(1)求y与x之间的函数关系式;
(2)如果装运每种水果的车辆数都不少于2辆,那么车辆的安排方案有哪几种?
(3)在(2)的条件下,若水果A每吨获得的利润与它的销售量有直接的关系a=x+12.5,要使这次组织销售的利润最大,应选用哪种方案?
分析:(1)根据题意列式:6x+5y+4(20-x-y)=100,变形后即可得到y=-2x+20;
(2)根据装运每种水果的车辆数都不少于2辆,x≥2,y≥2,解不等式组即可;
(3)根据题意列出利润与x之间的函数关系可发现是二次函数,利用二次函数的顶点公式即可求得最大值,根据实际意义可知整数x=6时,利润最大.
(2)根据装运每种水果的车辆数都不少于2辆,x≥2,y≥2,解不等式组即可;
(3)根据题意列出利润与x之间的函数关系可发现是二次函数,利用二次函数的顶点公式即可求得最大值,根据实际意义可知整数x=6时,利润最大.
解答:解:(1)设运A水果的车有x,运B水果的有y辆,则运C水果的有20-x-y辆,
所以,6x+5y+4(20-x-y)=100,
故y=-2x+20;
(2)∵装运每种水果的车辆数都不少于2辆,
∴x≥2,y=-2x+20≥2,
解得:2≤x≤9,
∴共8种方案:x=2,3,4,5,6,7,8,9;
(3)利润=6x(x+12.5)+5y×16+4(20-x-y)×10=6x2-45x+1600,
∵对称轴为x=-
=3
,
∴在6,5,4中,当x=6时,利润最大,
则要使这次组织销售的利润最大,运A水果的车有6辆,运B水果的有8辆,则运C水果的有6辆.
所以,6x+5y+4(20-x-y)=100,
故y=-2x+20;
(2)∵装运每种水果的车辆数都不少于2辆,
∴x≥2,y=-2x+20≥2,
解得:2≤x≤9,
∴共8种方案:x=2,3,4,5,6,7,8,9;
(3)利润=6x(x+12.5)+5y×16+4(20-x-y)×10=6x2-45x+1600,
∵对称轴为x=-
| b |
| 2a |
| 3 |
| 4 |
∴在6,5,4中,当x=6时,利润最大,
则要使这次组织销售的利润最大,运A水果的车有6辆,运B水果的有8辆,则运C水果的有6辆.
点评:主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意要根据自变量的实际范围确定函数的最值.

练习册系列答案
相关题目
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
(1)设装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
| 脐 橙 品 种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨脐橙获得(百元) | 12 | 16 | 10 |
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
|
脐 橙 品 种 |
A |
B |
C |
|
每辆汽车运载量(吨) |
6 |
5 |
4 |
|
每吨脐橙获得(百元) |
12 |
16 |
10 |
(1)设装运A种脐橙的车辆数为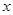 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为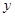 ,求
,求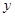 与
与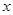 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值。
