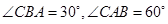题目内容
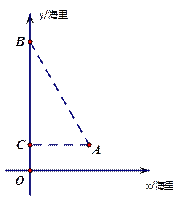
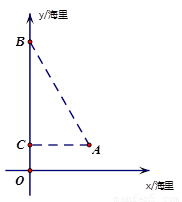
如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在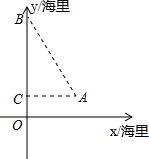 y轴上,且∠CBA=30°,∠CAB=60°.
y轴上,且∠CBA=30°,∠CAB=60°.(1)求这时船A与海岛B之间的距离;
(2)若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由.
分析:(1)证明△ABC是直角三角形,且AC=10.根据cos∠BAC=
即可求得AB的长;
(2)在直角△ACB中,tan∠BAC=
,即可求得BC的长,与16比较大小即可.
| AC |
| AB |
(2)在直角△ACB中,tan∠BAC=
| AC |
| AB |
解答:解:(1)∵∠CBA=30°,∠CAB=60°,
∴∠ACB=90°. (1分)
在Rt△ACB中,
∵cos60°=
,
∴AB=20(海里). (4分)
(2)在Rt△ACB中,
tan60°=
,
∴BC=10
>16海里,(6分)
∴无触礁危险. (7分)
∴∠ACB=90°. (1分)
在Rt△ACB中,
∵cos60°=
| AC |
| AB |
∴AB=20(海里). (4分)
(2)在Rt△ACB中,
tan60°=
| BC |
| AC |
∴BC=10
| 3 |
∴无触礁危险. (7分)
点评:本题主要考查了三角函数的定义,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目