题目内容
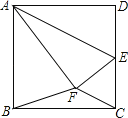
【题目】如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为 .
【答案】![]()
【解析】
试题分析:根据题意得出S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,进而得出S△BFC=FN,再利用勾股定理得出FN的长,进而得出答案.
解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,
∴△ADE≌△AFE,DE=EC=EF=2,AB=AF=4,
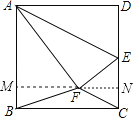
过点F作FN⊥CD于点N,FM⊥AB于点M,
∴S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,
∴![]() ×2×4+
×2×4+![]() ×2×4+
×2×4+![]() ×2×FN+
×2×FN+![]() ×4×(4﹣FN)+S△BFC=16,
×4×(4﹣FN)+S△BFC=16,
∴8+FN+8﹣2FN+S△BFC=16,
∴S△BFC=FN=![]() ×BC×NC=2NC,
×BC×NC=2NC,
设NC=x,则FN=2x,EN=2﹣x,
∴EF2=EN2+FN2,
∴22=(2﹣x)2+(2x)2,
解得:x1=0(不合题意舍去),x2=![]() ,
,
∴FN=2×![]() =
=![]() ,
,
∴S△BFC=![]() .
.
故答案为:![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目