题目内容
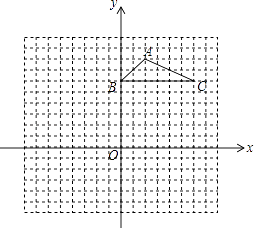
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示: 
(1)甲乙两地相距多远?
(2)求快车和慢车的速度分别是多少?
(3)求出两车相遇后y与x之间的函数关系式;
(4)何时两车相距300千米.
【答案】
(1)解:由图象得:甲乙两地相距600千米
(2)解:由题意得:慢车总用时10小时,
∴慢车速度为 ![]() =60(千米/小时);
=60(千米/小时);
想和快车速度为x千米/小时,
由图象得:60×4+4x=600,解得:x=90,
∴快车速度为90千米/小时,慢车速度为60千米/小时
(3)解:由图象得: ![]() =
= ![]() (小时),60×
(小时),60× ![]() =400(千米),
=400(千米),
时间为 ![]() 小时时快车已到达甲地,此时慢车走了400千米,
小时时快车已到达甲地,此时慢车走了400千米,
∴两车相遇后y与x的函数关系式为 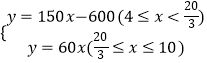
(4)解:设出发x小时后,两车相距300千米.
①当两车没有相遇时,
由题意得:60x+90x=600﹣300,解得:x=2;
②当两车相遇后,
由题意得:60x+90x=600+300,解得:x=6;
即两车2小时或6小时时,两车相距300千米
【解析】(1)由图象容易得出答案;(2)由题意得出慢车速度为 ![]() =60(千米/小时);设快车速度为x千米/小时,由图象得出方程,解方程即可;(3)求出相遇的时间和慢车行驶的路程,即可得出答案;(4)分两种情况,由题意得出方程,解方程即可.
=60(千米/小时);设快车速度为x千米/小时,由图象得出方程,解方程即可;(3)求出相遇的时间和慢车行驶的路程,即可得出答案;(4)分两种情况,由题意得出方程,解方程即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目