题目内容
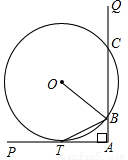
如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.
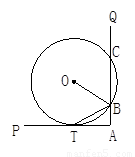
(1)BT是否平分∠OBA?证明你的结论.
(2)若已知AT=4,试求AB的长.
【答案】
(1)平分;(2)2
【解析】
试题分析:(1)连接OT,根据切线的性质可得∠OTA=90°,即可得到∠OBT=∠OTB=90°-∠ATB=∠ABT,从而得到结果;
(2)过O作OM⊥BC于M,则可得四边形OTAM是矩形,根据矩形的性质可得OM=AT=4,AM=OT=5.在Rt△OBM中,根据勾股定理可得BM的长,从而可以求得结果.
(1)连接OT,
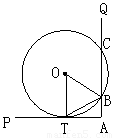
∵PT切⊙O于T,
∴OT⊥PT,故∠OTA="90°,"
从而∠OBT=∠OTB=90°-∠ATB=∠ABT.即BT平分∠OBA.
(2)过O作OM⊥BC于M
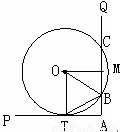
则四边形OTAM是矩形,
故OM=AT=4,AM=OT=5.在Rt△OBM中, OB=5,OM=4,
故BM=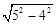 =3,从而AB=AM-BM=5-3=2.
=3,从而AB=AM-BM=5-3=2.
考点:切线的性质,角平分线的判定,矩形的判定和性质,勾股定理
点评:本题综合性强,知识点较多,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.

练习册系列答案
相关题目
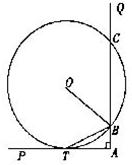 25、如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.
25、如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C. 如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点.
如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点. (2004•江西)如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.
(2004•江西)如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.