题目内容
（2004•江西）如图，∠PAQ是直角，半径为5的⊙O与AP相切于点T，与AQ相交于两点B、C．（1）BT是否平分∠OBA？
是
是
；（2）若已知AT=4，AB=
2
2
．分析：（1）连接OT，AT是切线，则OT⊥AP，可以证明AB∥OT，得到∠TBA=∠BTO，再根据等边对等角得到∠OTB=∠OBT，就可以证出结论；
（2）过点B作BH⊥OT于点H，然后在Rt△OBH中，利用OB=5，BH=AT=4根据勾股定理求出OH，最后即可求出AB．
（2）过点B作BH⊥OT于点H，然后在Rt△OBH中，利用OB=5，BH=AT=4根据勾股定理求出OH，最后即可求出AB．
解答：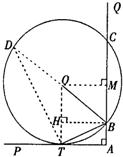
解：（1）BT平分∠OBA，
证明：连接OT，
∵AT是切线，
∴OT⊥AP．
又∵∠PAB是直角，即AQ⊥AP，
∴AB∥OT，
∴∠TBA=∠BTO．
又∵OT=OB，
∴∠OTB=∠OBT．
∴∠OBT=∠TBA，即BT平分∠OBA；
（2）过点B作BH⊥OT于点H，
则在Rt△OBH中，OB=5，BH=AT=4
∴OH=3，
∴AB=HT=OT-OH=5-3=2．
解：（1）BT平分∠OBA，证明：连接OT，
∵AT是切线，
∴OT⊥AP．
又∵∠PAB是直角，即AQ⊥AP，
∴AB∥OT，
∴∠TBA=∠BTO．
又∵OT=OB，
∴∠OTB=∠OBT．
∴∠OBT=∠TBA，即BT平分∠OBA；
（2）过点B作BH⊥OT于点H，
则在Rt△OBH中，OB=5，BH=AT=4
∴OH=3，
∴AB=HT=OT-OH=5-3=2．
点评：本题主要考查了切线的性质定理，以及等角对等边等知识，此题的解题方法比较多，灵活性比较高．
练习册系列答案
期末集结号系列答案
相关题目
