题目内容
两个相似三角形面积之差为9cm2,对应的中线的比是| 2 |
| 3 |
分析:有三角形对应中线的比可得三角形的面积比,再由面积之差建立等式,代入数据求解即可.
解答:解:∵两个三角形的对应的中线的比是
:
,
∴其面积之比为2:3,
可设其中一个的面积为2x,则另一个面积为3x,
又两个相似三角形面积之差为9cm2,
即3x-2x=9,解得x=9,
∴两个三角形的面积为2x=18cm2,3x=27cm2.
故答案为18cm2,27cm2.
| 2 |
| 3 |
∴其面积之比为2:3,
可设其中一个的面积为2x,则另一个面积为3x,
又两个相似三角形面积之差为9cm2,
即3x-2x=9,解得x=9,
∴两个三角形的面积为2x=18cm2,3x=27cm2.
故答案为18cm2,27cm2.
点评:本题主要考查了相似三角形的性质问题,即对应边与面积之间的关系,能够熟练掌握.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
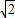 ,则较小三角形的对应边上的高为 .
,则较小三角形的对应边上的高为 .