题目内容
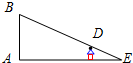 如图,当小颖从路灯AB的底部A点走到C点时,发现自己在路灯B下的影子顶部落在正前方E处.若AC=4m,影子CE=2m,小颖身高为1.6m,则路灯AB的高为
如图,当小颖从路灯AB的底部A点走到C点时,发现自己在路灯B下的影子顶部落在正前方E处.若AC=4m,影子CE=2m,小颖身高为1.6m,则路灯AB的高为
- A.4.8米
- B.4米
- C.3.2米
- D.2.4米
A
分析:根据题意可知△CDE和△ABE是相似三角形,运用相似比可求得AB的长.
解答:∵CD∥AB,
∴△CDE∽△ABE,
∴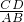 =
=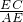 ,
,
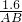 =
= ,
,
AB=4.8.
故选A.
点评:本题考查相似三角形的判定以及相似三角形的性质应用,利用相似比求线段的长.
分析:根据题意可知△CDE和△ABE是相似三角形,运用相似比可求得AB的长.
解答:∵CD∥AB,
∴△CDE∽△ABE,
∴
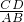 =
=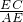 ,
,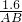 =
= ,
,AB=4.8.
故选A.
点评:本题考查相似三角形的判定以及相似三角形的性质应用,利用相似比求线段的长.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
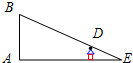 如图,当小颖从路灯AB的底部A点走到C点时,发现自己在路灯B下的影子顶部落在正前方E处.若AC=4m,影子CE=2m,小颖身高为1.6m,则路灯AB的高为( )
如图,当小颖从路灯AB的底部A点走到C点时,发现自己在路灯B下的影子顶部落在正前方E处.若AC=4m,影子CE=2m,小颖身高为1.6m,则路灯AB的高为( )| A、4.8米 | B、4米 | C、3.2米 | D、2.4米 |
