Question

【题目】在△ABC中，AB＝AC，D、E分别在BC和AC上，AD与BE相交于点F．

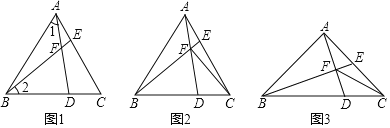
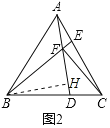
（1）如图1，若∠BAC＝60°，BD＝CE，求证：∠1＝∠2；

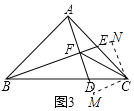
（2）如图2，在（1）的条件下，连接CF，若CF⊥BF，求证：BF＝2AF；

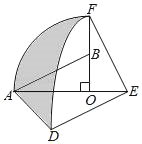
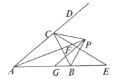
（3）如图3，∠BAC＝∠BFD＝2∠CFD＝90°，若S△ABC＝2，求S△CDF的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）根据等边三角形的判定定理得到△ABC为等边三角形，得到AB＝BC，∠ABC＝∠C＝60°，证明△ABD≌△BCE，根据全等三角形的性质证明结论；

（2）过B作BH⊥AD，根据全等三角形的性质得到∠BAD＝∠CBE，证明△AHB≌△BFC，根据全等三角形的性质解答；

（3）过C作CM⊥AD交AD延长线于M，过C作CN⊥BE交BE延长线于N，根据角平分线的性质得到CM＝CN，证明△AFB≌△CMA，根据全等三角形的性质得到BF＝AM，AF＝CM，根据三角形的面积公式列式计算即可．

（1）证明：∵AB＝AC，∠BAC＝60°，

∴△ABC为等边三角形，

∴AB＝BC，∠ABC＝∠C＝60°，

在△ABD和△BCE中，

，

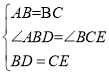∴△ABD≌△BCE（SAS），

∴∠1＝∠2；

（2）如图2，过B作BH⊥AD，垂足为H，

∵△ABD≌△BCE，

∴∠BAD＝∠CBE，

∵∠ABF+∠CBE＝60°，

∴∠BFD＝∠ABF+∠BAD＝60°，

∴∠FBH＝30°，

∴BF＝2FH，

在△AHB和△BFC中，

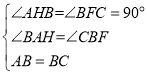
∴△AHB≌△BFC（AAS），

∴BF＝AH＝AF+FH＝2FH，

∴AF＝FH，

∴BF＝2AF；

（3）如图3，过C作CM⊥AD交AD延长线于M，过C作CN⊥BE交BE延长线于N，

∵∠BFD＝2∠CFD＝90°，

∴∠EFC＝∠DFC＝45°，

∴CF是∠MFN的角平分线，

∴CM＝CN，

∵∠BAC＝∠BFD＝90°，

∴∠ABF＝∠CAD，

在△AFB和△CMA中，

∴△AFB≌△CMA（AAS）

∴BF＝AM，AF＝CM，

∴AF＝CN，

∵∠FMC＝90°，∠CFM＝45°，

∴△FMC为等腰直角三角形，

∴FM＝CM，

∴BF＝AM＝AF+FM＝2CM，

∵

∴S△BDF＝2S△CDF，

∵AF＝CM，FM＝CM，

∴AF＝FM，

∴F是AM的中点，

∴ ，

∵AF⊥BF，CN⊥BF，AF＝CN，

∴S△AFB＝S△BFC，

设S△CDF＝x，则S△BDF＝2x，

∴S△AFB＝S△BFC＝3x

∴ ，

则3x+3x+x＝2，

解得，x＝，即S△CDF＝．