题目内容
 如图,点M是函数y=x+
如图,点M是函数y=x+| 1 | x |
分析:延长AM,交直线y=x于点D,则△AOD是等腰直角三角形,即∠ADO=45°,由于MB⊥l,所以由勾股定理可知MB=BD=
MD,设M点坐标为(x,x+
),由于M在第一象限,所以MA=x,OA=AD=x+
,所以MD=AD-AM=
,进而可求出答案.
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答: 解:延长AM,交直线y=x于点D,设M(x,x+
解:延长AM,交直线y=x于点D,设M(x,x+
)
则△AOD是等腰直角三角形,即∠ADO=45°,
∴OA=AD=x+
,AM=x,
∴MD=AD-AM=
,
∵MB⊥l,
∴MB=BD,
∴△BDM是等腰直角三角形,
∴MB2+BD2=MD2,
∴MB=
MD,
∴MB=
×
=
,
∴MA•MB=x•
=
.
故答案为:
.
 解:延长AM,交直线y=x于点D,设M(x,x+
解:延长AM,交直线y=x于点D,设M(x,x+| 1 |
| x |
则△AOD是等腰直角三角形,即∠ADO=45°,
∴OA=AD=x+
| 1 |
| x |
∴MD=AD-AM=
| 1 |
| x |
∵MB⊥l,
∴MB=BD,
∴△BDM是等腰直角三角形,
∴MB2+BD2=MD2,
∴MB=
| ||
| 2 |
∴MB=
| ||
| 2 |
| 1 |
| x |
| ||
| 2x |
∴MA•MB=x•
| ||
| 2x |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查的是反比例函数,涉及到正比例函数、等腰直角三角形的判定与性质及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题.

练习册系列答案
相关题目
 如图,点A是函数y=
如图,点A是函数y=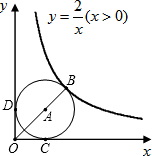 如图,点B是函数
如图,点B是函数
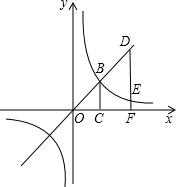 如图,点B是函数y=
如图,点B是函数y=