Question

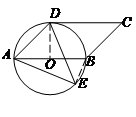
如图，在△ABC中，AB＝BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC， 交AB的延长线于E，垂足为F．

(1)求证：直线DE是⊙O的切线；
(2)当AB＝5，AC＝8时，求cosE的值．

Answer 1

（1）证OD⊥DE即可。（2）cosE=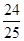

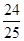
试题分析：如图，在△ABC中，AB＝BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC， 交AB的延长线于E，垂足为F．

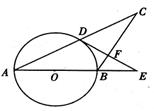
(1)连结OD。易知OA=OD=r，且AB＝BC，∴∠OAD=∠ODA=∠C
所以OD∥CB。所以∠ODE=∠BFE=90°。所以OD⊥DE，垂足为D。
所以直线DE是⊙O的切线。

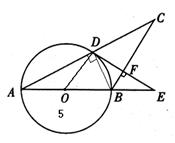
(2)当AB＝5，AC＝8时，求cosE的值．
解：连结BD。由（1）知OD⊥DE，又因为∠ADB=90°（直径所对圆周角）
所以∠ADO+∠ODB=∠ODB+∠BDE。因为OD∥CB，则∠ODB=∠DBO=∠DBF
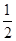所以Rt△ADB∽Rt△DFB。则，已知AB=BC，BD⊥AC。所以AD=AC=4.
所以在Rt△ADB中，BD=3.故3×3=5×BF，解得BF=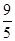。易知Rt△EDO∽Rt△EFB
则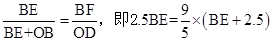，解得BE=
所以在Rt△EFB中，cosE＝
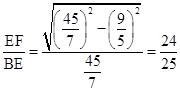
点评：本题难度较大，主要考查学生对圆的切线问题与三角形相似判定与性质的掌握。为中考常考题型要牢固掌握。