题目内容
在直角坐标系中,M为x轴正半轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为AB延长线上一点(不含B点),连接PC交⊙M于Q,连接DQ,若A(-1,0),C(0,
)

(1)求圆心M的坐标;
(2)过B点作BH⊥DQ于H,当P点运动时,线段CQ、QH、DH有何数量关系,证明你的结论;
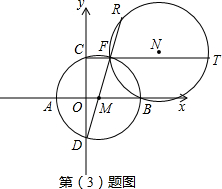
(3)R为⊙M的直径DF延长线上的一个动点(不包括F点),过B、F、R三点作⊙N,CF交⊙N于T,当R点在DF延长线上运动时,FT-FR的值是否变化?请说明理由.
| 3 |


(1)求圆心M的坐标;
(2)过B点作BH⊥DQ于H,当P点运动时,线段CQ、QH、DH有何数量关系,证明你的结论;
(3)R为⊙M的直径DF延长线上的一个动点(不包括F点),过B、F、R三点作⊙N,CF交⊙N于T,当R点在DF延长线上运动时,FT-FR的值是否变化?请说明理由.
分析:(1)连接MC、AC,根据A、C坐标求出∠CAM,得出等边三角形CAM即可;
(2)连接BC、BD,在DQ上截取DN=CQ,连接BN,由垂径定理求出CO=DO,CB=DB,根据SAS证△CQB≌△DNB,推出BN=BQ,求出QH=HN即可;
(3)连接BF、BT、BR,推出△FMB是等边三角形,得出BF=BM,∠FBM=60°,求出CF∥AB,推出∠TFB=∠FMB,加上∠R=∠T,得出△RBM≌△TBF,得出FT=MR,求出FT-FR=FM=2.
(2)连接BC、BD,在DQ上截取DN=CQ,连接BN,由垂径定理求出CO=DO,CB=DB,根据SAS证△CQB≌△DNB,推出BN=BQ,求出QH=HN即可;
(3)连接BF、BT、BR,推出△FMB是等边三角形,得出BF=BM,∠FBM=60°,求出CF∥AB,推出∠TFB=∠FMB,加上∠R=∠T,得出△RBM≌△TBF,得出FT=MR,求出FT-FR=FM=2.
解答: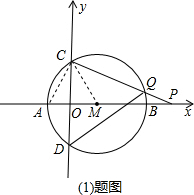 (1)解:连接MC、AC,
(1)解:连接MC、AC,
∵A(-1,0),C(0,
),
∴OA=1,OC=
,AC=
=2
tan∠CAB=
=
,
∴∠CAB=60°,
∵MA=MC,
∴△ACM是等边三角形,
∴MA=MC=AC=2,
∴OM=2-1=1,
即M的坐标是(1,0);
(2)线段CQ、QH、DH的数量关系是CQ=DH-HQ,
证明:连接BC、BD,在DQ上截取DN=CQ,连接BN,
∵AM⊥CD,
∴由垂径定理得:CO=DO,
∴CB=DB,
∵∠QCB和∠QDB都对弧BQ,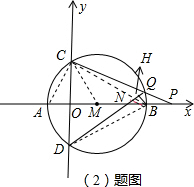
∴∠QCB=∠QDB,
∵在△CQB和△DNB中
,
∴△CQB≌△DNB,
∴BN=BQ,
∵BH⊥DQ,
∴QH=HN,
∴CQ=DN=DH-HN=DH-HQ,
即线段CQ、QH、DH的数量关系是CQ=DH-HQ;
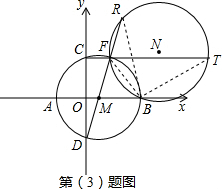 (3)解:FT-FR的值不变化,永远等于2,
(3)解:FT-FR的值不变化,永远等于2,
理由是:连接BF、BT、BR,
∵OM=1,OD=OC=
,
根据勾股定理得:DM=2,
即OM=
DM,
∴∠ODM=30°,
∴∠OMD=90°-30°=60°,
∴∠OMD=60°=∠FMB,
∵MF=MB,
∴△FMB是等边三角形,
∴BF=BM,∠FBM=60°,
∵DF为直径,
∴∠FCD=90°=∠COM,
∴CF∥AB,
∴∠TFB=∠FBM=60°=∠FMB,
∵弧BF对的圆周角是∠R和∠T,
∴∠R=∠T,
∵在△RBM和△TBF中
,
∴△RBM≌△TBF,
∴FT=MR,
∴FT-FR=MR-FR=MF,
∵C(0,
),m(1,0),
∴MF=MC=
=2
∴FT-FR=2,
即FT-FR的值不变化,恒等于2.
 (1)解:连接MC、AC,
(1)解:连接MC、AC,∵A(-1,0),C(0,
| 3 |
∴OA=1,OC=
| 3 |
(
|
tan∠CAB=
| OC |
| OA |
| 3 |
∴∠CAB=60°,
∵MA=MC,
∴△ACM是等边三角形,
∴MA=MC=AC=2,
∴OM=2-1=1,
即M的坐标是(1,0);
(2)线段CQ、QH、DH的数量关系是CQ=DH-HQ,
证明:连接BC、BD,在DQ上截取DN=CQ,连接BN,
∵AM⊥CD,
∴由垂径定理得:CO=DO,
∴CB=DB,
∵∠QCB和∠QDB都对弧BQ,

∴∠QCB=∠QDB,
∵在△CQB和△DNB中
|
∴△CQB≌△DNB,
∴BN=BQ,
∵BH⊥DQ,
∴QH=HN,
∴CQ=DN=DH-HN=DH-HQ,
即线段CQ、QH、DH的数量关系是CQ=DH-HQ;
 (3)解:FT-FR的值不变化,永远等于2,
(3)解:FT-FR的值不变化,永远等于2,理由是:连接BF、BT、BR,
∵OM=1,OD=OC=
| 3 |
根据勾股定理得:DM=2,
即OM=
| 1 |
| 2 |
∴∠ODM=30°,
∴∠OMD=90°-30°=60°,
∴∠OMD=60°=∠FMB,
∵MF=MB,
∴△FMB是等边三角形,
∴BF=BM,∠FBM=60°,
∵DF为直径,
∴∠FCD=90°=∠COM,
∴CF∥AB,
∴∠TFB=∠FBM=60°=∠FMB,
∵弧BF对的圆周角是∠R和∠T,
∴∠R=∠T,
∵在△RBM和△TBF中
|
∴△RBM≌△TBF,
∴FT=MR,
∴FT-FR=MR-FR=MF,
∵C(0,
| 3 |
∴MF=MC=
12+(
|
∴FT-FR=2,
即FT-FR的值不变化,恒等于2.
点评:本题考查了全等三角形的性质和判定,勾股定理,锐角三角函数的定义,等边三角形的性质和判定,圆周角定理,垂径定理等知识点的应用,主要考查学生运用定理进行推理的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
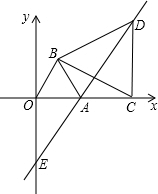 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.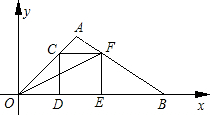 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.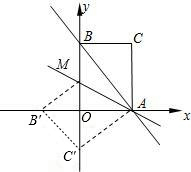 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.