Question

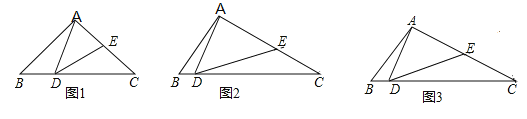
【题目】如图，△ABC内接于⊙O，BC＝2，AB＝AC，点D为上的动点，且cos∠ABC＝．

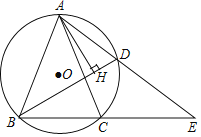
（1）求AB的长度；

（2）在点D的运动过程中，弦AD的延长线交BC延长线于点E，问ADAE的值是否变化？若不变，请求出ADAE的值；若变化，请说明理由；

（3）在点D的运动过程中，过A点作AH⊥BD，求证：BH＝CD+DH．

Answer 1

【答案】（1）AB＝；（2）不变，ADAE＝10；（3）见解析

【解析】

（1）作AM垂直于BC，由AB＝AC，利用三线合一得到BM等于BC的一半，再由cos∠ABC的值，利用锐角三角函数定义求出AB的长即可；

（2）连接DC，由等边对等角得到∠ACB＝∠ABC，结合圆内接四边形的性质得到∠ADC＝∠ACE，然后证明△EAC∽△CAD，由相似得比例求出所求即可；

（3）在BD上取一点N，使得BN＝CD，利用SAS得到△ABN≌△ACD，由全等三角形对应边相等和等腰三角形的性质求出NH＝HD即可得出结论．

解：（1）作AM⊥BC，

∵AB＝AC，AM⊥BC，

∴BM＝BC＝1，

∵cos∠ABC＝，

∴AB＝；

（2）连接DC，

由（1）知AB＝AC＝，

∴∠ACB＝∠ABC，

∵四边形ABCD内接于圆O，

∴∠ADC+∠ABC＝180°，

∵∠ACE+∠ACB＝180°，

∴∠ADC＝∠ACE，

∵∠CAE＝∠DAC，

∴△EAC∽△CAD，

∴，

∴ADAE＝AC2＝10；

（3）在BD上取一点N，使得BN＝CD，

在△ABN和△ACD中，，

∴△ABN≌△ACD（SAS），

∴AN＝AD，

∵AH⊥BD，

∴NH＝HD，

∵BN＝CD，NH＝HD，

∴BN+NH＝CD+HD，

即BH＝CD+DH．