题目内容
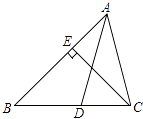
【题目】如图,在锐角△ABC中,AB=4 ![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ). 
A.3
B.4
C.5
D.6
【答案】B
【解析】解答:如图,在AC上截取AE=AN,连接BE.
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中, 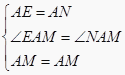 ,
,
∴△AME≌△AMN(SAS),
∴ME=MN.
∴BM+MN=BM+ME≥BE.
∵BM+MN有最小值.
当BE是点B到直线AC的距离时,BE⊥AC,
又AB=4 ![]() ,∠BAC=45°,此时,△ABE为等腰直角三角形,
,∠BAC=45°,此时,△ABE为等腰直角三角形,
∴BE=4,
即BE取最小值为4,
∴BM+MN的最小值是4.
所以答案是:B.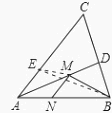
分析:从已知条件结合图形认真思考,通过构造全等三角形,利用三角形的三边的关系确定线段和的最小值.
【考点精析】根据题目的已知条件,利用三角形的“三线”和轴对称-最短路线问题的相关知识可以得到问题的答案,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目