题目内容
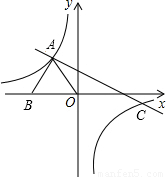
如图已知,△OAB中,AB=AO=5,OB=6,双曲线 过点A,直线y=kx+b与双曲线
过点A,直线y=kx+b与双曲线 ,相交于A、C两点,且C点的横坐标为6.
,相交于A、C两点,且C点的横坐标为6.①求点A的坐标;②求双曲线
 与直线AC的解析式.
与直线AC的解析式.
【答案】分析:①由在△OAB中,AB=AO=5,OB=6,可以解出点A的坐标;
②点A在双曲线上,求出k值,又知点C在双曲线上,C点的横坐标为6,求出C点坐标,由两点式求出直线AC的解析式.
解答: 解:①过AD⊥x轴,交点为D,
解:①过AD⊥x轴,交点为D,
在△OAB中,AB=AO=5,OB=6,
∴OD= OB=3,AD=
OB=3,AD=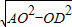 =4,
=4,
∴A点坐标为(-3,4);
②∵点A在双曲线上,
∴k=-12,
∴双曲线的解析式为:y=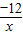 ,
,
∵点C在双曲线上,C点的横坐标为6,
∴y=-2,
∴D点坐标为(6,-2),
∴直线AC的解析式为:y=- x+2.
x+2.
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数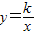 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
②点A在双曲线上,求出k值,又知点C在双曲线上,C点的横坐标为6,求出C点坐标,由两点式求出直线AC的解析式.
解答:
 解:①过AD⊥x轴,交点为D,
解:①过AD⊥x轴,交点为D,在△OAB中,AB=AO=5,OB=6,
∴OD=
 OB=3,AD=
OB=3,AD=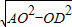 =4,
=4,∴A点坐标为(-3,4);
②∵点A在双曲线上,
∴k=-12,
∴双曲线的解析式为:y=
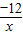 ,
,∵点C在双曲线上,C点的横坐标为6,
∴y=-2,
∴D点坐标为(6,-2),
∴直线AC的解析式为:y=-
 x+2.
x+2.点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数
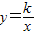 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义. 
练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1
21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1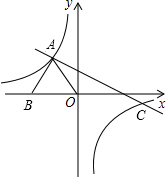 如图已知,△OAB中,AB=AO=5,OB=6,双曲线
如图已知,△OAB中,AB=AO=5,OB=6,双曲线 如图已知,△OAB中,AB=AO=5,OB=6,双曲线
如图已知,△OAB中,AB=AO=5,OB=6,双曲线 过点A,直线y=kx+b与双曲线
过点A,直线y=kx+b与双曲线 过点A,直线y=kx+b与双曲线
过点A,直线y=kx+b与双曲线 ,相交于A、C两点,且C点的横坐标为6.
,相交于A、C两点,且C点的横坐标为6. 与直线AC的解析式.
与直线AC的解析式.