ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŅ»Õų¤·½ŠĪÖ½ĢõÉĻ»Ņ»ĢõŹżÖį£®
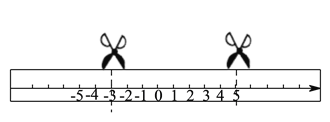
£Ø![]() £©ČōÕŪµžÖ½Ģõ£¬ŹżÖįÉĻ±ķŹ¾
£©ČōÕŪµžÖ½Ģõ£¬ŹżÖįÉĻ±ķŹ¾![]() µÄµćÓė±ķŹ¾
µÄµćÓė±ķŹ¾![]() µÄµćÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£®
µÄµćÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£®
£Ø![]() £©Čō¾¹żÄ³“ĪÕŪµžŗó£¬øĆŹżÖįÉĖµÄĮ½øöŹż
£©Čō¾¹żÄ³“ĪÕŪµžŗó£¬øĆŹżÖįÉĖµÄĮ½øöŹż![]() ŗĶ
ŗĶ![]() ±ķŹ¾µÄµćĒ”ŗĆÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£ØÓĆŗ¬
±ķŹ¾µÄµćĒ”ŗĆÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£ØÓĆŗ¬![]() £¬
£¬ ![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
£Ø![]() £©Čō½«“ĖÖ½ĢõŃŲŠéĻß“¦¼ōæŖ£¬½«ÖŠ¼äµÄŅ»¶ĪÖ½Ģõ¶ŌÕŪ£¬Ź¹Ęä×óÓŅĮ½¶ĖÖŲŗĻ£¬ÕāŃłĮ¬Šų¶ŌÕŪ
£©Čō½«“ĖÖ½ĢõŃŲŠéĻß“¦¼ōæŖ£¬½«ÖŠ¼äµÄŅ»¶ĪÖ½Ģõ¶ŌÕŪ£¬Ź¹Ęä×óÓŅĮ½¶ĖÖŲŗĻ£¬ÕāŃłĮ¬Šų¶ŌÕŪ![]() “Īŗó£¬ŌŁ½«ĘäÕ¹æŖ£¬Ēė·Ö±šĒó³ö×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£ØÓĆŗ¬
“Īŗó£¬ŌŁ½«ĘäÕ¹æŖ£¬Ēė·Ö±šĒó³ö×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£ØÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
”¾“š°ø”æ(1)-1;(2) ![]() ;(3)
;(3) ![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÕŅ³ö5±ķŹ¾µÄµćÓė-3±ķŹ¾µÄµć×é³ÉĻ߶ĪµÄÖŠµć±ķŹ¾Źż£¬Č»ŗó½įŗĻŹżÖį¼“æÉĒóµĆ“š°ø£»
£Ø2£©ĻČÕŅ³öa±ķŹ¾µÄµćÓėb±ķŹ¾µÄµćĖł×é³ÉĻ߶ĪµÄÖŠµć£¬“Ó¶ųæÉĒóµĆ“š°ø£»
£Ø3£©ĻČĒó³öĆæĮ½ĢõĻąĮŚÕŪŗŪµÄ¾ąĄė£¬½ųŅ»²½µĆµ½×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£¬¼“æÉĒóµĆ“š°ø£®
ŹŌĢā½āĪö£ŗ£Ø![]() £©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ
£©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ![]() ŗĶ
ŗĶ![]() µÄÖŠµć
µÄÖŠµć![]() £®
£®
£Ø![]() £©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ
£©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ![]() ŗĶ
ŗĶ![]() µÄÖŠµć
µÄÖŠµć![]() £®
£®
£Ø![]() £©×ī×ó¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ
£©×ī×ó¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ ![]() £®×īÓŅ¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ
£®×īÓŅ¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ ![]() £®
£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æij°ą”°ŹżŃ§ŠĖȤŠ”×é”±¶ŌŗÆŹży=x2©2|x|µÄĶ¼ĻóŗĶŠŌÖŹ½ųŠŠĮĖĢ½¾æ£¬Ģ½¾æ¹ż³ĢČēĻĀ£¬Ēė²¹³äĶźÕū£®£Ø1£©×Ō±äĮæxµÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬xÓėyµÄ¼ø×é¶ŌÓ¦ÖµĮŠ±ķČēĻĀ£ŗ
x | ” | ©3 | © | ©2 | ©1 | 0 | 1 | 2 |
| 3 | ” |
y | ” | 3 |
| m | ©1 | 0 | ©1 | 0 |
| 3 | ” |
ĘäÖŠ£¬m=””””£®
£Ø2£©øł¾Ż±ķÖŠŹż¾Ż£¬ŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠĆčµć£¬²¢»³öĮĖŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£¬Ēė»³öøĆŗÆŹżĶ¼ĻóµÄĮķŅ»²æ·Ö£®
£Ø3£©¹Ū²ģŗÆŹżĶ¼Ļ󣬊“³öĮ½ĢõŗÆŹżµÄŠŌÖŹ£®
£Ø4£©½ųŅ»²½Ģ½¾æŗÆŹżĶ¼Ļó·¢ĻÖ£ŗ
¢ŁŗÆŹżĶ¼ĻóÓėxÖįÓŠ””””øö½»µć£¬ĖłŅŌ¶ŌÓ¦µÄ·½³Ģx2©2|x|=0ÓŠ”” ””øöŹµŹżøł£»
¢Ś·½³Ģx2©2|x|=2ÓŠ””””øöŹµŹżøł.

¢Ū¹ŲÓŚxµÄ·½³Ģx2©2|x|=aÓŠ4øöŹµŹżøłŹ±£¬aµÄȔֵ·¶Ī§ŹĒ”” £®
”¾ĢāÄæ”æ°“ĻĀĮŠ³ĢŠņ¼ĘĖć£¬°Ń“š°øĢīŠ“ŌŚ±ķøńĄļ£¬Č»ŗóæ“æ“ÓŠŹ²Ć“¹ęĀÉ£¬ĻėĻėĪŖŹ²Ć“»įÓŠ
Õāøö¹ęĀÉ£æ
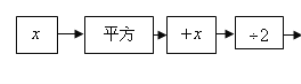

£Ø1£©ĢīŠ“±ķÄŚæÕøń£ŗ
ŹäČė | 3 | 2 | £2 |
| ” |
Źä³ö“š°ø | 0 | ” |
£Ø2£©Äć·¢ĻֵĹęĀÉŹĒ____________.
£Ø3£©ÓĆ¼ņŅŖ¹ż³ĢĖµĆ÷Äć·¢ĻֵĹęĀɵÄÕżČ·ŠŌ.

