题目内容
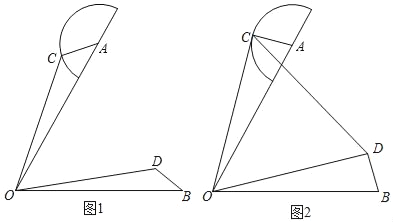
【题目】已知OA=OB=4,∠AOB=60°,半⊙A的半径为1,点C是半圆上任意一点,连结OC,把OC绕点O顺时针旋转6
0°到OD的位置,连结BD.
(1)如图1,求证:AC=BD.
(2)如图2,当OC与半圆相切于点C时,求CD的长.
(3)直接写出△AOC面积的最大值.
【答案】(1)详见解析;(2)![]() ;(3)2.
;(3)2.
【解析】
(1)根据已知条件易证△OAC≌△DOB,由全等三角形的性质即可得AC=BD;(2)根据勾股定理求得OC的长,再证明△COD是等边三角形,根据等边三角形的性质即可得CD的长;(3)当h最大时,S△AOC最大,即当C在半圆A的中点时,h最大,此时h=1,计算面积可得结论.
证明:(1)∵∠AOB=∠COD=60°
∴∠COA+∠AOD=∠BOD+∠AOD
∴∠COA=∠BOD
在△OAC和△OBD中,
∵
∴△OAC≌△DOB(SAS)
∴AC=BD;
(2)如图2,∵OC是⊙A的切线,
∴AC⊥OC,∠OCA=90°,
在Rt△OCA中,由勾股定理得:OC2+AC2=OA2,
∴OC2+12=42,
∴OC=![]() ,
,
在△COD中,∵OC=OD,∠COD=60°,
∴△COD是等边三角形,
∴CD=OC=![]() ;
;
(3)设点C到OA的距离为h,
∵S△AOC=![]() OAh,
OAh,
∵OA=4,
∴当h最大时,S△AOC最大,即当C在半圆A的中点时,h最大,此时h=1,
∴S△AOC=![]() OAh=
OAh=![]() =2.
=2.

练习册系列答案
相关题目