题目内容
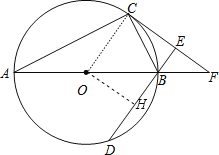
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若⊙O的半径为![]() cm,弦BD的长为3cm,求CF的长.
cm,弦BD的长为3cm,求CF的长.

考点:切线的判定.
【答案】
【解析】
试题分析:(1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)解:作OH⊥BD于H,如图,根据垂径定理得到BH=DH=![]() BD=
BD=![]() ,在Rt△OBH中可利用勾股定理计算出OH=2,易得四边形OHEC为矩形,则CE=OH=2,HE=OC=
,在Rt△OBH中可利用勾股定理计算出OH=2,易得四边形OHEC为矩形,则CE=OH=2,HE=OC=![]() ,BE=1,然后证明△FBE∽△FOC,利用相似比可计算出CF.
,BE=1,然后证明△FBE∽△FOC,利用相似比可计算出CF.
(1)证明:连结OC,如图,
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)解:作OH⊥BD于H,如图,
则BH=DH=![]() BD=
BD=![]() ,
,
在Rt△OBH中,∵OB=![]() ,BH=
,BH=![]() ,
,
∴OH=![]() =2,
=2,
易得四边形OHEC为矩形,
∴CE=OH=2,HE=OC=![]() ,
,
∴BE=NE﹣BH=1,
∵BE∥OC,
∴△FBE∽△FOC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目