Question

著名数学教育家G．波利亚，有句名言：“发现问题比解决问题更重要”，这句话启发我们：要想学好数学，就需要观察，发现问题，探索问题的规律性东西，要有一双敏锐的眼睛．请先观察、计算再填空．
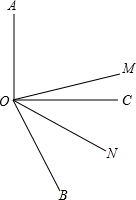
已知：如图，OM平分∠AOB，ON平分∠BOC．
（1）当∠AOC=90°，∠BOC=70°时，∠MON=______；
（2）当∠AOC=80°，∠BOC=60°时，∠MON=______；
（3）当∠AOC=70°，∠BOC=50°时，∠MON=______；
（4）猜想：不论∠AOC和∠BOC的度数是多少，∠MON的度数总等于______度数的一半．

Answer 1

解：（1）∵∠AOC=90°，∠BOC=60°，
∴∠AOB=90°+60°=150°，
∵OM平分∠AOB，
∴∠AOM=∠AOB=75°，
∴∠MOC=90°-75°=15°，
又∵ON平分∠BOC，
∴∠NOC=∠BOC=30°，
∴∠MON=∠MOC+∠NOC=15°+30°=45°，
故答案为：45°；

（2）∵∠AOC=80°，∠BOC=60°，
∴∠AOB=80°+60°=140°，
∵OM平分∠AOB，
∴∠AOM=∠AOB=70°，
∴∠MOC=80°-70°=10°，
又∵ON平分∠BOC，
∴∠NOC=∠BOC=30°，
∴∠MON=∠MOC+∠NOC=10°+30°=40°，
故答案为：43°；

（3）∵∠AOC=70°，∠BOC=50°，
∴∠AOB=70°+50°=120°，
∵OM平分∠AOB，
∴∠AOM=∠AOB=60°，
∴∠MOC=70°-60°=10°，
又∵ON平分∠BOC，
∴∠NOC=∠BOC=25°，
∴∠MON=∠MOC+∠NOC=10°+25°=35°，
故答案为：35°；

（4）由以上（1）（2）（3）得出结论∠MON=∠AOC，
故答案为：∠AOC．
分析：（1）已知∠AOC，∠BOC，OM平分∠AOB，ON平分∠BOC；则得到∠NOC=∠BOC，∠AOM=∠MOB，要求∠MON，先求出∠MOC和∠NOC；
（2）由OM平分∠AOB，求出∠AOM，再求出∠MOC，再由ON平分∠BOC求出∠NOC，从而求出∠MON；
（3）已知OM平分∠AOB，ON平分∠BOC，所以可求出∠AOM，∠NOC，再求出∠MOC，从而求出∠MON；
（4）由（1）（2）（3）可得出结论．
点评：此题考查的知识点是角平分线的定义及角的计算，关键是根据角平分线定义得出所求角与已知角的关系转化求解．