题目内容
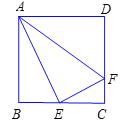
【题目】如图，在正方形ABCD中，E是BC的中点，F是线段CD上的动点.
(1)如图1，若CF=
CD，求证：ΔAEF是直角三角形；
(2)如图2，若点F与点D重合，点G在ED上，且AG=AD，求证：
.
【答案】（1）详见解析；（2）详见解析.
【解析】
（1）利用正方形的性质得出AB=BC=CD=DA，∠B=∠C=∠D=90°，设出边长为a，进一步利用勾股定理求得AE、EF、AF的长，再利用勾股定理逆定理判定即可；
（2）过点A作AH⊥GD，垂足为H，因为AG=AD，所以GH=HD，根据勾股定理表示出AE2、AH2，代入即可得出结论.
解：（1）设正方形ABCD的边长为a，则
∵
∴
∴△AEF是以E为直角顶点的直角三角形
（2）如图，过点A作AH⊥GD，垂足为H，
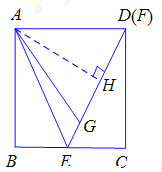
∵AG=AD
∴GH=HD
在Rt△AEH中：
在Rt△ADH中：
∴
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
